Now that we know that water is important to life and that stars have different luminosities it is important to consider at what distance from a star a planet can be habitable. At present we only have a single example of a habitable planet to use for comparison (i.e. Earth), however, physics and climate modelling can be used to estimate where the Circumstellar Habitable Zone (CHZ) lies.

In order to calculate the position of the CHZ it is necessary to answer three questions:
- What levels of irradiance allow liquid water to exist on a planet’s surface?
- How luminous is the star the planet orbits?
- At what distance from this star would a planet experience habitable levels of irradiance?
The first question is a simplification that assumes habitability requires liquid water on the surface and that the only heat source to provide this is light from a sun. This does not account for tidal heating providing heat or a possible habitable zone in the upper regions of the atmosphere, for example. For most purposes, this is a reasonable approach though.
If a planet is too close to its sun then it may end up like Venus with a runaway greenhouse effect that boils any water and renders the surface hot and uninhabitable. Alternatively, if the planet is too far away from its sun it will be a frozen icy rock. However, between these two extremes life can perhaps flourish.
There are many scientific papers discussing how to calculate the inner and outer limits of this CHZ, however, I have chosen to use one entitled Strong Dependence Of The Inner Edge Of The Habitable Zone On Planetary Rotation Rate. This paper consider how a slowly rotating (or tidally locked) planet can experience different levels of irradiance to a faster rotating planet and yet still be habitable. This is of particular interest as Khthonia is tidally locked and rotates much slower than Earth.
The following chart uses the results from this paper and shows how the level of illumination (relative to the amount the Earth receives from the Sun) that produces habitability is linked to the temperature of the star. For reference, the amount of illumination the Earth receives from the Sun is known as the Solar constant and is approximately 1,360 Watts per square metre. For simplicity it is much easier to measure irradiance relative to this value since we know Earth is habitable and expect other habitable planets to have approximately the same value.
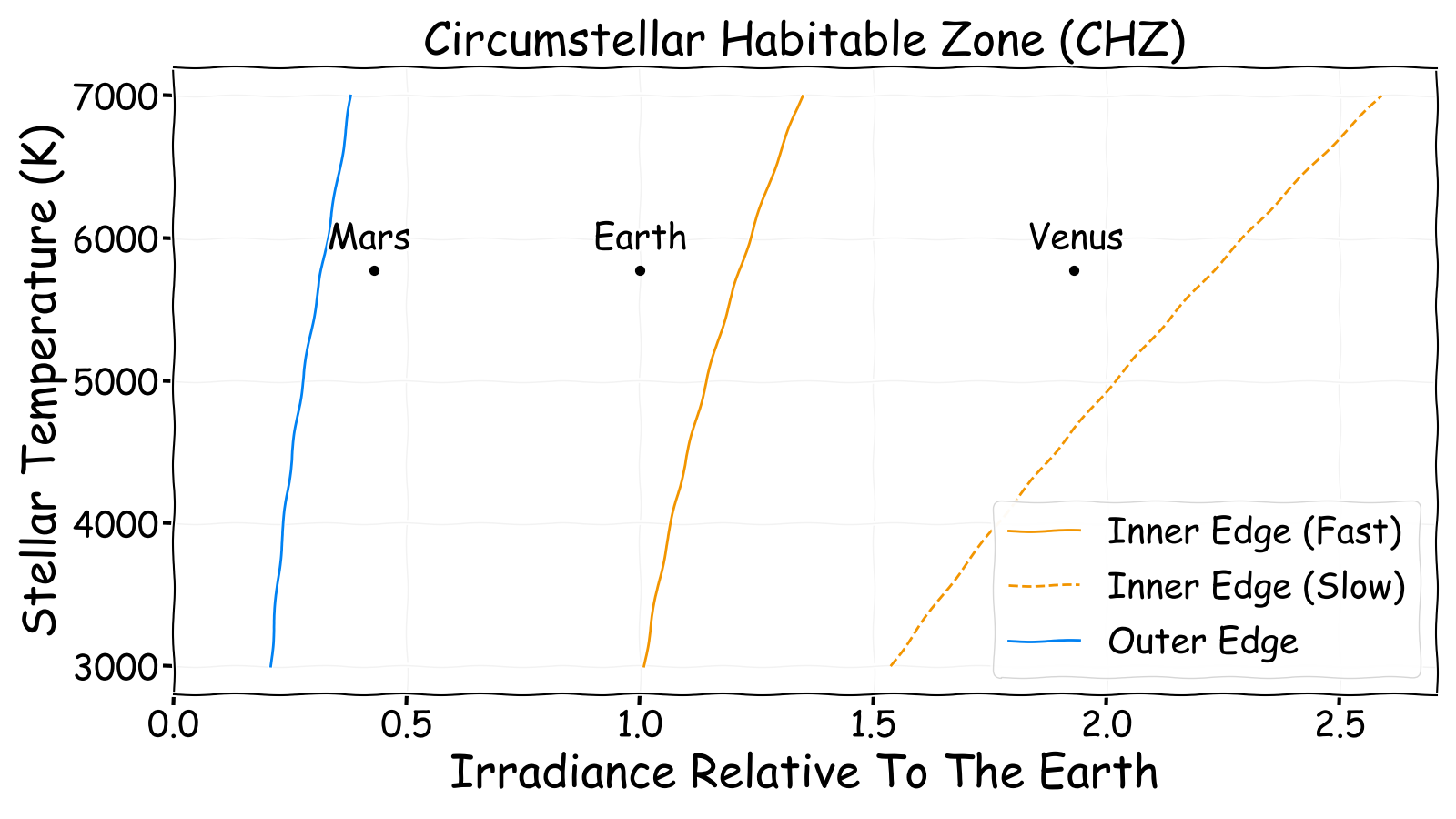
The reason for the sensitivity to the temperature of the star is due to change in the emission spectrum. Cooler stars produce a greater proportion of their illumination as infrared and this heats up a planet to greater extent than the blue dominated light from hotter stars. Therefore, for a fixed level of irradiance a cool star could render a planet uninhabitable whereas a hotter star would not.
The sensitivity of the inner habitable limit to rotation rate is slightly more subtle. If a planet is slowly rotating then the side facing the sun will heat up significantly. This has the effect of evaporating large quantities of water which forms clouds. These clouds reflect light away from the planet surface which prevents the planet overheating. The greater the stellar illumination, the more clouds are formed and the greater the cooling effect. This is an example of a negative feedback that can stabilise the climate.
In order to produce a habitable planet it is therefore necessary to select an irradiance relative to the Earth’s that lies within the habitable zone for a star of that temperature. Once this is known, it is then possible to calculate the distance from the star a planet must be to receive this level of illumination.
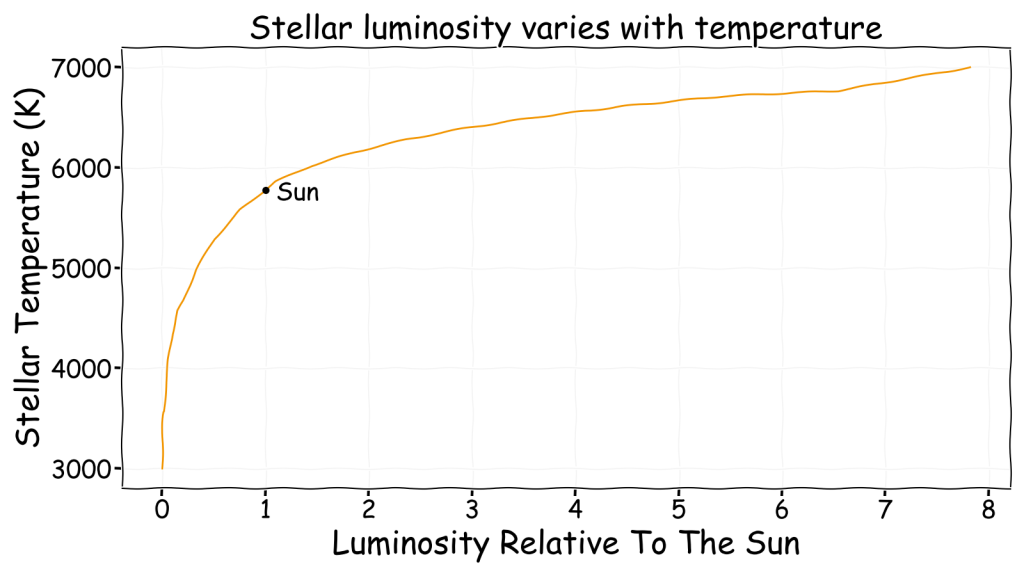
The next step in calculating the location of the habitable zone is to calculate how luminous the star is. The luminosity of a star can be calculated by using the Stefan-Boltzmann law which states that the power radiated is proportional to the fourth power of the temperature. I.e. if temperature of a star doubles (and nothing else changes) then the luminosity would increase sixteen fold (i.e. 2 x 2 x 2 x 2). Similarly, if the surface area of a star changes (and nothing else) then the luminosity would increase proportionally. This means that luminosity is proportional to the radius squared, i.e. a star with twice the radius has four times the luminosity.
For the mathematically inclined you can estimate a star’s luminosity with the following equation:
\[L = 4pi R^2\sigma T^4\]
L is the luminosity in watts, R is the stellar radius in metres, σ is the Stefan-Boltzmann constant and T is the stellar temperature in kelvin.
It is however simpler to work in relative units and consider a star’s luminosity relative to the Sun’s luminosity which is defined to be 3.828 x 1026 W and given the symbol L☉. This means that a star’s luminosity relative to the Sun can be calculated with the following relationship where the stellar radius is also relative to the Sun’s radius:
\[Luminosity = Radius^2\left(\frac{Temperature}{Solar\;Temperature}\right)^4\]
However, from a previous post we know that the mass, temperature and luminosity of a star are linked. For simplicity, the relationship used to produce the charts in the previous post can also be used to estimate luminosity versus temperature without worrying about the radius or mass.
We now know the minimum and maximum levels of irradiance for various stellar temperatures that would produce a habitable planet. We also know the star’s luminosity for various stellar temperatures. By linking this information it is possible to determine at what distance from a star a planet can orbit and still be habitable.
The stellar irradiance received at a planet’s position is determined by two factors, the stellar luminosity and the distance from the planet to the star. If the luminosity is half that of the Sun then a planet the same distance from its sun as Earth is from the Sun will receive half the irradiance. Due to the inverse-square law if a planet is twice as far from its sun then it will receive only a quarter of the irradiance. Combining this leads to the following relationship:
\[Irradiance = \frac{Luminosity}{Distance^2}\]
This is again in relative units so that irradiance is in multiples of the solar constant, luminosity is relative to the Sun’s luminosity and distance is measured in astronomical units (AU) where the Earth is 1 AU from the Sun. We now only need to rearrange this relationship to be able to calculate the planetary distance that corresponds to a particular irradiance:
\[Distance = \sqrt{\frac{Luminosity}{Irradiance}}\]
Putting this all together finally produces a chart of habitable zone distance versus stellar temperature.
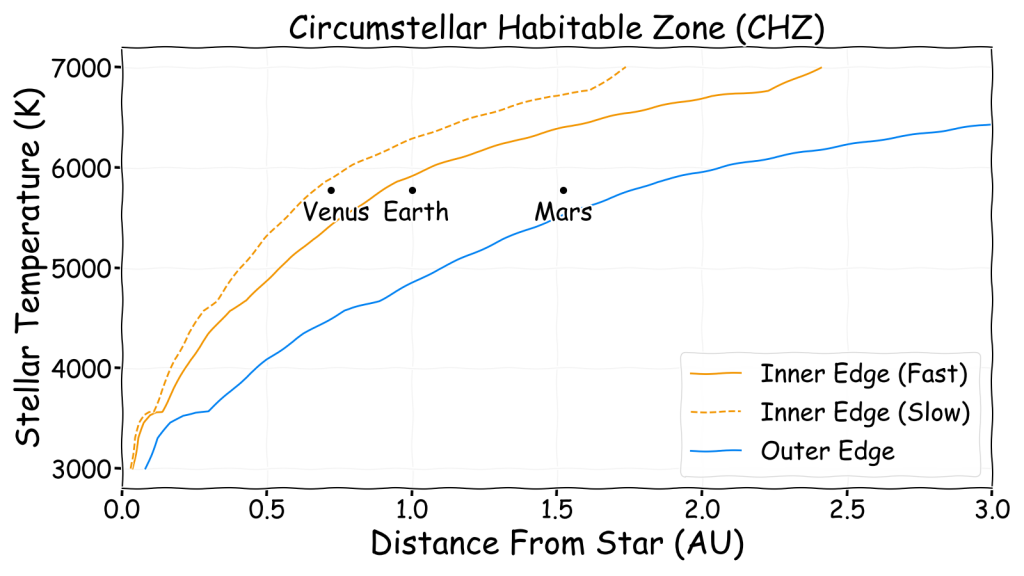
The result is a bit “wobbly” (yes, that’s a technical term) for low stellar temperatures but it does give an indication of how far away a planet can be from a star and still be habitable based on stellar illumination alone.
Hopefully, this post provides some information on where to position a planet around a star in order that it can plausibly be considered to be habitable. I’ve tried to stay clear from complicated equations and use charts and simple relationships to provide some guidance. Let me know in the comments if this is useful or not.
