In response to a question on the Speculative Evolution Forum and my previous post on the Circumstellar Habitable Zone I thought I would discuss a simple model to calculate the average temperature of a planet. I will first present a model that doesn’t account for the greenhouse effect and then extend it to include an idealised version of the greenhouse effect. In practice there are many other modifications that could be made to make a more accurate model but I’m not a professional climatologist. That’s what the Met Office is for!
Background
In order to calculate how hot a planet would be based on the nature of its host star and its distance from it requires knowledge of a few physics concepts. For this reason, this post will contain more than a few equations. I imagine that some readers will be fine with this and others will not. Please let me know in the comments your opinion on this. If you want to avoid them you can just skim to the summary section at the end but do try to look at the pretty graphs along the way.
Black Bodies
A key concept in calculating the average temperature of a planet is that of a Black Body. This was previously mentioned in the post discussing what colour are stars. A black body is a physics term for an object that is a perfect absorber of light and absorbs all light that it receives. By Kirchhoff’s law of thermal radiation this means that it is also a perfect emitter.
The amount of energy a black body emits across all wavelengths can be determined solely from its temperature using Planck’s Law. The following equation defines the spectral radiance emitted from black body in terms of emitted power per unit emitting area per unit solid angle per wavelength (Wsr-1m-3)
\[B(\lambda,T) = \frac{2hc^2}{\lambda^5}\cfrac{1}{e^\cfrac{hc}{\lambda k_BT}-1}\]
where \(\lambda\) is the wavelength, \(T\) is the temperature, \(h\) is the Planck constant, \(c\) is the speed of light and \(k_B\) is the Boltzmann constant.

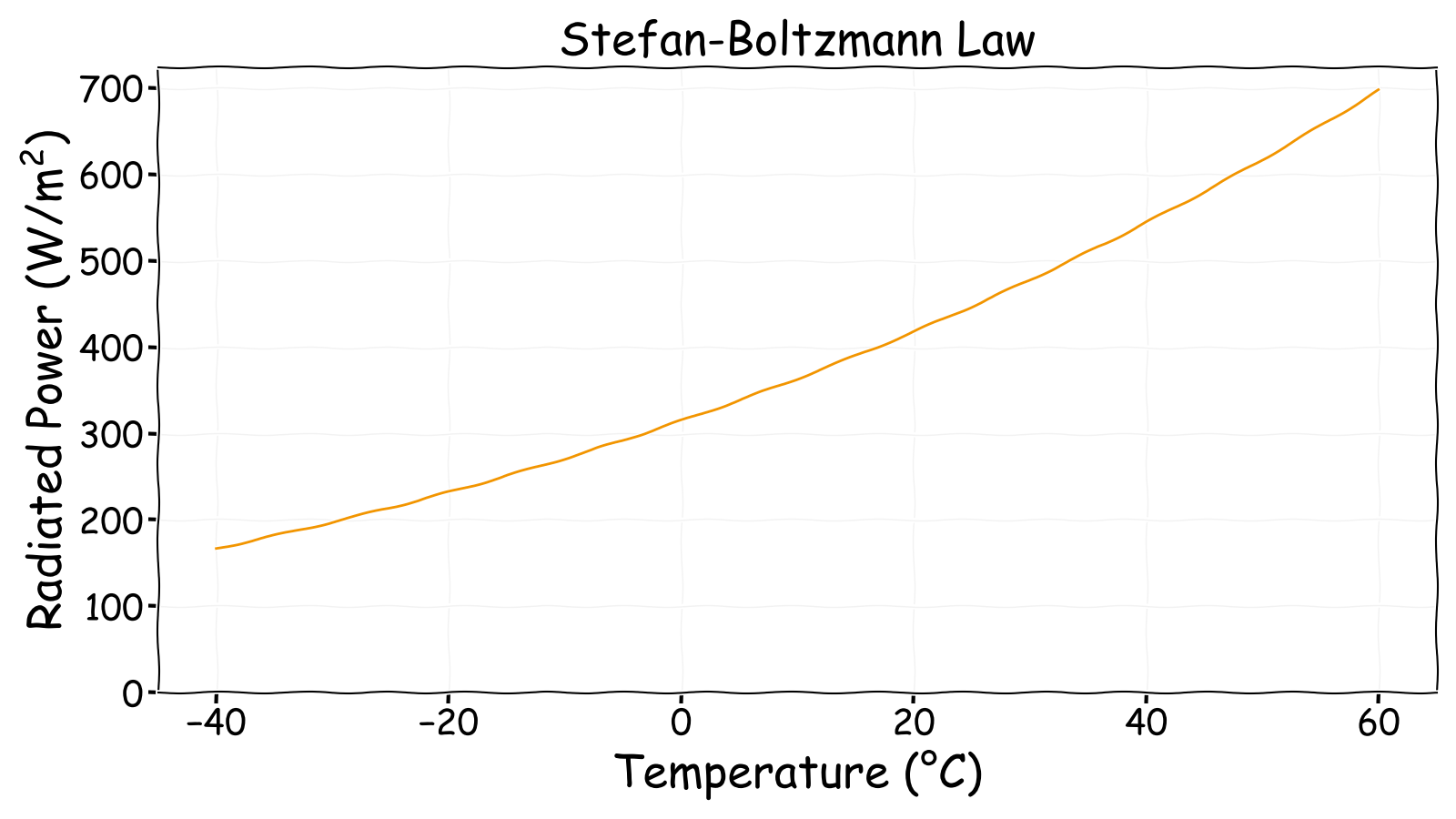
However, of more use for calculating the temperature of a planet is the Stefan-Boltzmann law. This defines the total radiated power per unit area (Wm-2) from a black body in terms of its temperature. Effectively, it sums the power produced at each wavelength according to the Planck curve
\[F = \sigma T^4\]
where (sigma) is the Stefan-Boltzmann constant.
Grey Bodies
While black bodies are a useful theoretical concept an ideal black body cannot actually exist. Some objects are sufficiently close that it is accurate enough to treat them as a black body, but most objects do not absorb all light that falls on them but instead reflect some light. Since they are not perfect absorbers this also means that they are not perfect emitters.
A non-perfect emitter can be treated as a grey body, with an emissivity somewhere between 0 and 1. The emissivity represents how closely the object resembles a perfect black body. An object with an emissivity of 1 is a perfect absorber (i.e. a black body) whereas an emissivity of 0 represents a perfect reflector. The emissivity of a material is used to modify the Stefan-Boltzmann law to produce a lower power output as compared to a black body
\[F = \epsilon \sigma T^4\]
where \(\epsilon\) is the emissivity. Many natural materials have an emissivity close to 1, so in practice the power emitted by a grey body is often only slightly lower than for a black body at the same temperature.
Wavelength Dependence
Of course, even a grey body is a simplification of reality. Real objects typically have an emissivity that varies with wavelength., i.e. they are coloured. However, treating all room temperature solids and liquids as grey bodies is sufficiently accurate for most purposes. Gases on the other hand have an emissivity that can vary significantly with wavelength. This is most easily demonstrated by looking at the atmospheric absorption versus wavelength for the region where ambient temperature objects emit energy according to Planck’s law.

This shows that at some wavelengths the atmosphere is opaque (i.e. high absorption) and at others it is transparent (i.e. low absorption). Between about 8 and 14 μm the atmosphere is transparent and this allows the heat emitted by ambient temperature objects (according to Planck’s Law) to mostly escape. However, even in this region, there are specific wavelengths that still have a high absorption. These are caused by specific gases, in particular, water vapour (H2O) and carbon dioxide (CO2) are two important contributors to atmospheric absorption. Since they absorb the emitted heat from the surface and prevent it radiating into space and cooling the planet they are also significant contributors to the greenhouse effect.
However, a full analysis taking this wavelength dependence into account is far beyond the simple models I wish to investigate here. It is also extremely unlikely to be necessary for world building purposes and it begins to venture into the domain of professional climatology which is certainly not my aim here.
Simple Model
The simple model for calculating the temperature of a planet is to first calculate the amount of power absorbed from the planet’s star (or stars) and then to calculate the temperature of the planet that would emit the same amount of power. If these two numbers are equal then it means the planet is in thermal equilibrium and the resulting temperature is the planetary equilibrium temperature. Note that for the purposes of these calculations the absorbed and emitted power will be in terms of flux (i.e. power per unit surface area).

The flux absorbed is simply the flux received from the star minus the amount reflected
\[F_{abs} = (1 – \alpha) F_{star}\]
where \(\alpha\) is the planetary albedo. This is the proportion of starlight that is reflected from the planet and therefore it does not contribute to the heating of the planet. Earth’s albedo is about 0.3 which averages the albedos of land, sea, ice and clouds.
The flux received from the star can be found via the equivalent of the solar constant which is the power per unit area at the point in space where the planet is. The flux on the planet is found by multiplying by the planet’s cross section to get the total power received and dividing by the surface area
\[F_{star} = S \frac{\pi r^2}{4\pi r^2} = \frac{S}{4}\]
where \(r\) is planet’s radius and \(S\) is the solar constant. The solar constant can be defined via the star’s luminosity spread over a sphere with a radius equivalent to the planet’s distance from its sun
\[S = \frac{L}{4\pi a^2}\]
where \(L\) is the star’s luminosity and \(a\) is the distance between the planet and the star. I have previously discussed how a star’s luminosity is related to its mass so it is possible to just a select a luminosity value and use it in the equations. However, if you want to go a bit further you can instead define the star’s luminosity in terms of its radius and temperature by assuming it is a black body
\[L = 4\pi R^2 \sigma T^4_{star}\]
where \(R\) is the star’s radius and \(T_{star}\) is the star’s temperature.
These equations can all be combined to lead to the final equation for the absorbed power
\[F_{abs} = \frac{(1 – \alpha) L}{16\pi a^2}\]
The next step is to calculate the emitted radiation. This is quite simple using the Stefan-Boltzmann law and the planetary equilibrium temperature. However, we will consider the Earth to be a grey body and not a black body so we have to include emissivity to get the following relationship
\[F_{emit} = \epsilon \sigma T^4_{eq}\]
When in equilibrium the absorbed and emitted flux are the same, so by rearranging you can get the following relationship for the temperature of the planet
\[T_{eq} = \sqrt[4]{\frac{(1 – \alpha) L}{16\pi\epsilon\sigma a^2}}\]
Alternatively, you can calculate the planet’s distance from the star necessary to achieve a specific temperature
\[a = \sqrt{\frac{(1 – \alpha) L}{16\pi\epsilon\sigma T^4_{eq}}}\]
This model can be verified by using the following values appropriate for Earth showing that an equilibrium temperature of 288 K is found at 1 AU which is correct for Earth.
- \(\alpha = 0.30\)
- \(L = 3.83\text{ x }10^{26}\text{ W}\)
- \(\epsilon = 0.612\)
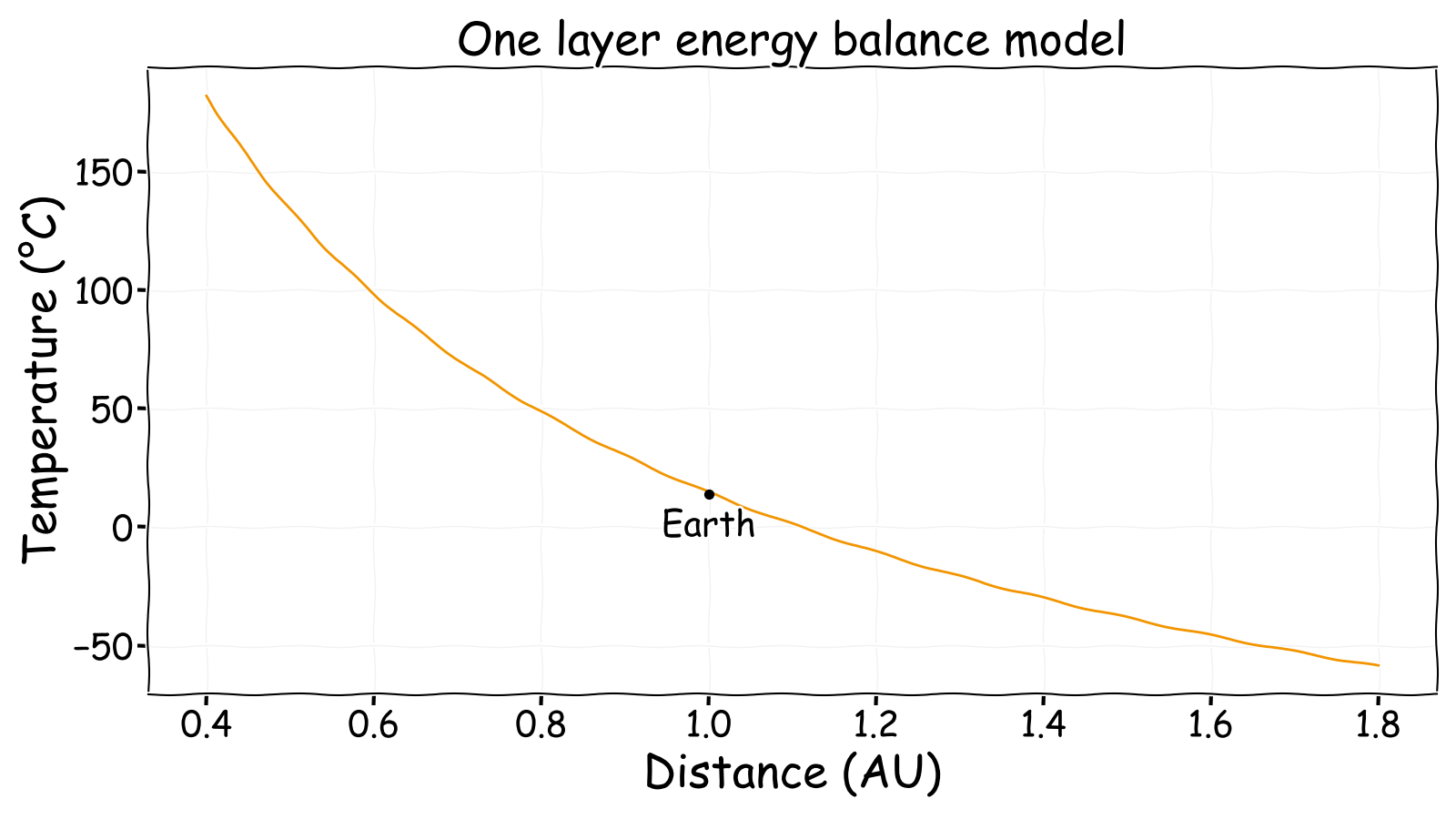
This simple model is perfectly acceptable to investigate the temperature versus distance relationship for Earth-like systems. It is also possible to change the albedo by considering some average value based on the fractional coverage of different surface types, e.g.:
- \(\alpha_{water} = 0.06\)
- \(\alpha_{vegetation} = 0.20\)
- \(\alpha_{sand} = 0.40\)
- \(\alpha_{snow} = 0.80\)
The albedo of clouds should also be accounted for but otherwise the atmosphere is treated as transparent to the incoming illumination. In reality, the atmosphere is not transparent to the outgoing emitted heat and therefore the value used for the emissivity should include the Greenhouse Effect.
In fact, the model suggests that increasing the emissivity would decrease the equilibrium temperature as the planet could radiate the same amount of energy as it received from the star at a lower temperature. This is backwards as increasing the concentration of greenhouse gases increases the emissivity of the atmosphere and also increases the temperature. Clearly a more complicated model is needed.
Idealised Greenhouse Model
An improved idealised greenhouse model is to treat the surface and the atmosphere separately. This two layer model uses a transparent-grey assumption where the atmosphere is transparent to incoming illumination from the star but is treated as a grey body for the outgoing thermal radiation. This is a valid assumption as on a habitable planet the illumination from the star will always be at a different wavelength to the planetary thermal radiation. It would only be an inaccurate assumption if the planet was a similar temperature to the star and this would clearly not be a habitable planet.
In this two layer model the incoming starlight is treated exactly as before with some fraction being reflected from the surface. Slightly confusingly, this also includes reflection from clouds despite the fact that clouds are in the atmosphere not on the surface. This does not cause any problems with the model however as the atmosphere is assumed to be transparent.
In contrast, the outgoing radiation from the surface has to pass through the atmosphere where some portion is absorbed which heats the atmosphere. As a grey body, the atmosphere then produces thermal radiation where half is emitted into space and half is emitted back towards the surface. The surface is assumed to be a black body and therefore absorbs all the thermal radiation from the atmosphere, heating up in the process until an equilibrium is reached.

This surface heating caused by atmospheric thermal emission is the greenhouse effect. If atmospheric absorption is lower then the heating effect is smaller and if atmospheric absorption is increased then the heating effect is larger. This explains why carbon dixode, water vapour, methane and ozone are the primary contributors to the greenhouse effect as they are significant contributors to atmospheric absorption.
Calculating all these contributions and balancing the incoming and outgoing power gives the following equation for the surface temperature, though I will leave the derivation as an exercise for the reader…
\[T_{eq} = \sqrt[4]{\frac{(1 – \alpha)L}{16\pi\sigma a^2}\cfrac{1}{1-\frac{\epsilon}{2}}}\]
As before, this can be rearranged to determine the distance between the star and planet to achieve a specified temperature
\[a = \sqrt{\frac{(1 – \alpha) L}{16\pi\sigma T^4_{eq}}\cfrac{1}{1-\frac{\epsilon}{2}}}\]
This can again be verified against Earth with the same parameters as before except with a slightly different emissivity which corresponds solely to the atmospheric emissivity.
- \(\alpha = 0.30\)
- \(L = 3.83\text{ x }10^{26}\text{ W}\)
- \(\epsilon = 0.78\)
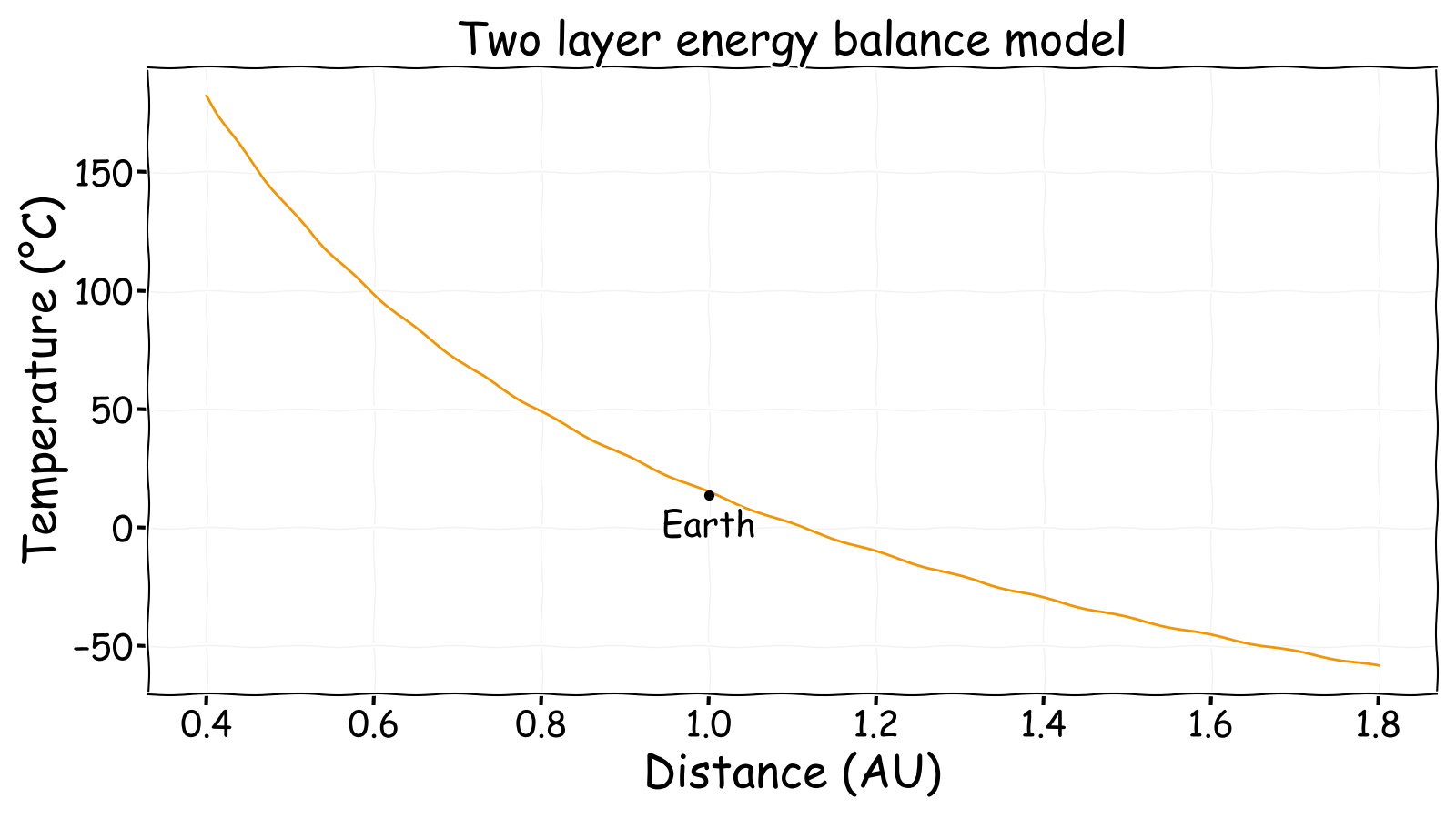
Since this looks exactly the same, this may not seem to be much more useful than the previous model. However, at least now increasing the emissivity causes the temperature to increase. This corresponds with the expected outcome whereby increasing greenhouse gas concentrations result in higher surface temperatures.
Atmospheric Emissivity
The final step in answering the original question is to determine how the emissivity varies with different atmospheric compositions. For simplicity only CO2 will be considered. Anything more than that becomes rather more complicated to analyse and probably isn’t necessary for most world building anyway.
There appears to be limited information on how emissivity varies with CO2 concentration, however, conveniently a paper entitled Radiation Transfer Calculations and Assessment of Global Warming by CO2 contains some values. These values can be plotted and a logarithmic curve can be fit to the values to allow the emissivity to be calculated at arbitrary values. Note that the previous emissivity value of 0.78 had been selected to match the measured Earth temperature and may not be the “true” value.

The logarithmic fit has two parameters and takes the following form
\[\epsilon = k \log_{10}(C) + \epsilon_0\]
\(\epsilon\) is the modelled emissivity, \(k\) is the scaling constant, \(C\) is the atmospheric CO2 concentration in ppm and \(\epsilon_0\) is the emissivity with no carbon dioxide present. Fitting this to the data produces the following parameters:
- \(k\) = 0.028
- \(\epsilon_0\) = 0.754
This is clearly not a perfect fit and it is an underestimate at higher concentrations but this is just an estimate not rigorous science after all. It is important to note that after all of this work it turns out that the emissivity only varies slightly with increasing CO2 anyway.
The final outcome is that it is possible to estimate the distance a planet should be from a star for a desired surface temperature and carbon dioxide concentration. This is obviously not a rigorous and accurate model but it seems more than sufficient for a world building exercise to ensure some level of scientific plausibility. It does seem approximately similar to some climate change predictions though the temperature change shown below does seem small unless large quantities of CO2 are present.

Summary
In summary, the aim was to calculate how far a planet should be from its sun in order to have a specified average surface temperature. Using a “simple” model the following steps allow this to be achieved:
- Define star luminosity.
- Define planetary albedo.
- Define planetary carbon dioxide concentration.
- Calculate atmospheric emissivity.
- Define desired planetary temperature.
- Solve equation below to calculate the necessary distance between the star and the planet.
\[a = \sqrt{\frac{(1 – \alpha) L}{16\pi\sigma T^4_{eq}}\cfrac{1}{1-\frac{\epsilon}{2}}}\]
It is important to remember that is still a “toy model” that is higher simplified relative to the climate on a real planet. I’m certainly not claiming that it is accurate or that it can be used for real science. However, it may still be useful for designing a planet where things at least seem somewhat realistic.
There are of course many further extensions that could be made and it’s not entirely impossible that I might revisit these at some point if there is a need.
- Tidal and internal radioactive heating could be added to the illumination flux.
- Habitability varies with the wavelength of the stellar illumination.
- The model assumes heat is even distributed over the planet’s surface but this is not true for a tidally locked planet
- More sophisticated atmospheres than an Earth-like atmosphere with a varied amount of carbon dioxide could be considered
- Time varying illumination due to eccentricity or multiple stars
Finally, I should apologise for the delay in writing this fairly length post. Covid-19, Christmas and Childcare have all combined to significantly reduce my free time since December. This has consequently reduced my blog writing productivity.
EDIT: Since writing this article I came across an alternative approach and wrote a quick post about this alternative carbon dioxide calculation. This alternative method is simply for many cases but isn’t as flexible.

quite very interesting; i think i understood/followed more than I'd assumed I would at the outset, so thank you for making and sharing this.
-anthony docimo
Thanks. This was deliberately equation heavy due to the post on the forum I was responding to. I know that's not what everybody wants but it's good to know it was understandable.
This is really good! I remember trying to read about and understand some of these equations over the summer, but I ended up getting stuck. Thank you for explaining them really well. I can't wait till I have time to start applying them to my own world building.
I'm glad you liked it and that it helped you. The basic model to calculate the planetary equilibrium temperature is adequate most of the time but it's good to go through the slightly more complicated models to better understand what is happening.
Hey there, fantastic post as always. I’ve long been looking for a simple model of greenhouse effect and I very much thank you for your contribution.
However I must confess myself confused by that ϵ=klog10(C)+ϵ0 equation. Plugged in with the numbers you give, the current CO2 concentration of 380 ppm taken as reference in the paper you link gives ϵ = 0.826 and 1-(ϵ/2) = 0.587, one too high and the other too low compared to the ϵ you gave as example either time.
I tried rederiving the equation from the paper for myself, but alas, my ignorance of physics works against me. The most promising dataset I found in the paper is at page 5, but it doesn’t seem to give an emissivity associated to CO2 concentrations at all, and I found no way of calculating one from the given quantities. If I may ask, how did you derive it?
Apologies for the delay, for some reason your post got marked as spam, though it is obviously VERY different to all the spam comments as you aren’t trying to sell me something!
The emissivity values in the one and two layer models are really just aggregate emissivity values that give the correct result for a particular model. It’s basically because the climate is more complicated than just one or two layers, so that simplification merges several parameters. The resulting emissivity isn’t really the emissivity of the atmosphere. In fact, if you modelled the atmosphere with multiple layers then you would have a decreasing emissivity with altitude. Therefore, technically an emissivity value can only be used with the same model that it is linked to. The CO2 data comes from a paper that uses a two-layer model, but I think it is slightly more complicated than my model, so the emissivity isn’t quite the same.
The data on page 5 gives the absorptivity (a) but from Kirchhoff’s Law this is equal to the emissivity. That’s why a blackbody is both a perfect absorber and a perfect emitter.
In practice it rapidly becomes a bit too complex for worldbuilding or speculative evolution purposes. I only launched myself down the rabbit hole due to the my response on the forum. The alternative approach in the following article is in some ways better as it clearly shows that you can have almost any temperature with any solar flux if you have the correct amount of carbon dioxide in the atmosphere.
Thanks for this this is a really great blog, I’m not sure if your still replying to this but I have a kind of stupid question. I’m trying to put these numbers into excel and I’m stuck on the Stefan Boltzmann Constant I think and what that number is exactly. I’ve put this value into excel “=5.6703744119*10^-8” but I don’t think that is right as my answers don’t agree with yours at all.