Giant Bags of Mostly Gas: Physics

It seems that one of the most common speculative evolution questions is whether or not lighter-than-air organisms (aka gasbags) are viable. I therefore thought I should write a comprehensive post on the subject to act as a general reference. Ironically, the length of my draft inflated to a large size as it turned out I had a lot to say on this. For this reason I will split this review of gasbags in to three parts. This first part covers the basic physics of buoyancy and how various parameters can provide more lift. The following parts will cover the anatomy of gasbags and an example of how several gasbag species could fit together to form an aerial ecosystem.

Gasbag Series Articles

• Part 1: Physics
• Part 2: Aeroplankton

Background

Lighter-than-air organisms floating in the clouds around gas giants are a fairly common trope in science fiction, from Sir Arthur Conan Doyle’s The Horror of the Heights* in 1913 to the more recent animated film Titan AE*. They have also been a feature in speculative science, perhaps most famously in Carl Sagan’s 1967 Nature letter on Venus and his 1976 NASA report on Jupiter.

Speculative evolution has taken this further with the most comprehensive analysis found in many articles over several years on the Planet Furaha blog. Lighter-than-air organisms are referred to as ballonts on that blog but here I will refer to them as “gasbags”. This is partially in reference to the Star Trek: The Next Generation episode, Home Soil, where a silicon based organism refers to humans as

Ugly ugly giant bags of mostly water

As you will see, any lighter-than-air organism will mostly be a bag of gas, but I don’t think that means they look ugly.

Zeppelin sized floating sky whales are perhaps the most common form of gasbags presented but for them to be viable there must be an entire perpetually floating ecosystem. The smallest members of this ecosystem would be some form of aeroplankton. These would not be lighter than air and would mainly rely on thermal updrafts or being carried in water droplets to remain the air. However, for the remaining gasbags there are several example size ranges:

• Small: (e.g. an aerial photosynthetic plant)
• Medium: (e.g. a herbivorous grazing jelly fish)
• Large: (e.g. an active shark like hunter)
• Giant: (e.g. a filter feeding sky whale)

While there are an infinite number of environments such organisms could exist in, three extraterrestrial environments will be considered along with Earth:

• Earth-like (1 bar, 273 K, nitrogen-oxygen atmosphere)
• The cloudy troposphere of Jupiter (5 bar, 300 K, hydrogen-helium atmosphere)
• The high altitude “habitable” cloud region on Venus (0.9 bar, 342 K, carbon dioxide atmosphere)
• The cold hazy atmosphere of Titan (1.4 bar, 92 K, nitrogen-methane atmosphere)

Now, I apologise in advance that this post will contain a lot of charts. For those who don’t wish to do the maths themselves this felt like the best way to provide a useful resources for other speculative evolution projects. Please let me know whether or not this was a good approach.

Buoyancy

Physics 

The basis of gasbags’ ability to float is buoyancy. This is the upward force exerted on an object by the gas or liquid it is immersed in. If this is sufficiently large then it can counter gravity and allow the organism to remain stationary or float upwards. Obviously, most gasbags are likely to have some level of control over their altitude but for the purposes of this analysis the important point is neutral buoyancy where the upward buoyancy force exactly matches the downward force of gravity.

A simple explanation of how buoyancy works was provided by Archimedes in around 246 BC:

Any object, totally or partially immersed in a fluid or liquid, is buoyed up by a force equal to the weight of the fluid displaced by the object.

This produces the following relatively simple relationship

\[\operatorname{apparent\_weight} = \operatorname{organism\_weight} – \operatorname{displaced\_air\_weight}\]

For a neutrally buoyant gas bag this implies the organism’s weight has to be equal to the displaced air weight (i.e. zero apparent weight). This also shows that the strength of gravity on a planet has no direct effect on the viability of a gasbag. If gravity increases then the weight of a neutrally buoyant gasbag will change by exactly the same amount as the weight of the displaced air.

For this reason it is clearer to change from weight to mass at this point, so for a neutrally buoyant gasbag

\[\operatorname{organism\_mass} = \operatorname{displaced\_air\_mass}\]

At this stage, the gas bag can be considered to be three distinct components:

1. The balloon membrane containing the lifting gas
2. The lifting gas within the balloon membrane
3. The rest of the organism (i.e. the body)

This leads to the following relationship for a neutrally buoyant gasbag

\[\operatorname{membrane\_mass} + \operatorname{lifting\_gas\_mass} + \operatorname{body\_mass} = \operatorname{displaced\_air\_mass}\]

Rearranging this leads to the key relationship showing how the displaced air provides lift and the lifting gas plus the membrane reduce this to leave just the neutrally buoyant body mass.

\[\operatorname{body\_mass} = \operatorname{displaced\_air\_mass} – \operatorname{lifting\_gas\_mass} – \operatorname{membrane\_mass}\]

For simplicity I will assume that the volume of displaced air is equal to the volume of lifting gas. This is not entirely accurate for two reasons. Firstly, the body will also displace some air and provide a little extra lift. Secondly, since the membrane has a finite thickness the volume of lifting gas will be smaller than the total volume of the balloon which reduces the lift slightly. These effects are quite small though so the model is reasonably accurate and more than sufficient for speculative evolution and world building purposes.

\[\begin{align}\operatorname{body\_mass} =\ &\operatorname{balloon\_volume} * (\operatorname{air\_density} – \operatorname{lifting\_gas\_density}) \\&- \operatorname{membrane\_surface\_area} * \operatorname{membrane\_area\_density}\end{align}\]

This relationship is the core of the gasbag condition. Increasing the density difference between air and lifting gas is the key to making a more massive body neutrally buoyant. If more lift is required then a larger balloon is necessary though this will also increase the membrane area.

Key Results

Hopefully, using words for the variables in the above equations made it slightly more reader friendly for a wider audience. Unfortunately, they are getting quite long so for this final step I will use normal algebra to represent the two key equations used to produce realistic gasbags more concisely.

As I am a physicist I will assume that the balloon is a sphere. Not only is this simpler, a sphere contains the most lifting gas for the least membrane so it will provide the most optimistic estimate for the gas bag body mass. This is reasonable for smaller gasbags but for larger ones they may be more blimp-like as this would reduce drag when moving. I’ll leave it as an exercise for the reader to calculate equivalent equations for an ellipsoidal balloon. Wikipedia has sufficient information for that but the equations are rather less neat.

This leads to the first equation that can be called the “neutrally buoyant mass equation” (equation 1). This defines the body mass of a neutrally buoyant gasbag for a given radius and set of densities (i.e. atmosphere, lifting gas and membrane density).

\[M_b = \frac{4 \pi R_m^3}{3}(\rho_a – \rho_l) – 4 \pi R_m^2 \rho_m\]

In this equation \(M_b\) is the neutrally buoyant body mass, \(R_m\) is the radius of the balloon membrane, \(\rho_a\) is the density of the air, \(\rho_l\) is the density of the lifting gas and \(\rho_m\) is the area density (i.e. mass per area) of the membrane.

This reveals why small balloons cannot be neutrally buoyant. The upward force is proportional to the balloon radius cubed (i.e. volume) whereas the downward component is proportional to the radius squared (i.e. area). This suggests a possible problem for small gasbags as the mass of the membrane area may be too large for the small volume of lifting gas to lift. This will be less of a problem for large gasbags because if the radius of the balloon doubles the lift component will increase by a factor of 8 but the membrane mass will only increase by a factor of 4.

This can be made slightly clearer by rearranging equation 1 and defining the difference in air and lifting gas densities as \(\Delta_\rho\). This gives the following

\[M_b = \frac{4 \pi R_m^2}{3}\left[R_m\Delta_\rho – 3\rho_m\right] \]

It then becomes clear that a zero mass body (i.e. \(M_b = 0\)) is achievable when the two terms in square brackets are equal. This leads to the “minimum radius equation” (equation 2) which defines the smallest possible balloon radius with no body mass for a set of density parameters

\[R_{min} = \frac{3 \rho_m}{\Delta_\rho}\]

This means the minimum radius scales linearly with membrane density, i.e. if the membrane density doubles then so does the minimum radius.

These two equations will now be used to investigate under what conditions a gasbag is viable as will be seen in the sections below. I will try to cover a wide range but it is impossible to cover all situations. These two equations should allow you to design plausible gasbags yourself.

Lifting Gas

The first factor to investigate is what lifting gas is used inside the balloon. This can be any gas or mixture of gases at all but it must be less dense than the air outside the balloon otherwise it won’t provide lift. Due to its widespread use in party balloons, everyone knows that helium is a possible lifting gas. However, Helium is unlikely to be available in large quantities to a gasbag.

Hydrogen is also an option, though it is rarely used in airships in modern times due to the flammability issues demonstrated by the 1937 Hinderburg disaster. Hydrogen can be biologically produced however as can methane, the third lifting gas option.

The density of a gas will vary with ambient temperature (e.g. higher temperature means lower density) and pressure (e.g. higher pressure means higher density) conditions, but for simplicity we can use the Standard Temperature and Pressure (STP) of 0°C and 1 bar. This is little cooler than ambient temperature on Earth in general but also slightly lower pressure. On balance this produces slightly lower densities and therefore slightly smaller gasbags but it’s fine for illustrative purposes.

• Air: 1.2754 kg/m³
• Methane: 0.716 kg/m³
• Helium: 0.1786 kg/m³
• Hydrogen: 0.08988 kg/m³

For reference, the absolute best “lifting gas” would be a pure vacuum as this has the lowest density possible (i.e. zero). This leads to the concept of a vacuum balloon. The problem with this is that the membrane must resist the compression caused by external air pressure. Any reinforcing elements designed to do that will add weight. The simplest way to prevent balloon collapse is of course to fill the balloon with a lower density gas at the same pressure.

For comparison the following chart shows the achievable neutrally buoyant body mass versus balloon radius for each of the three lifting gases under STP conditions. A “magic” massless membrane is used to provide an upper estimate on what is possible.

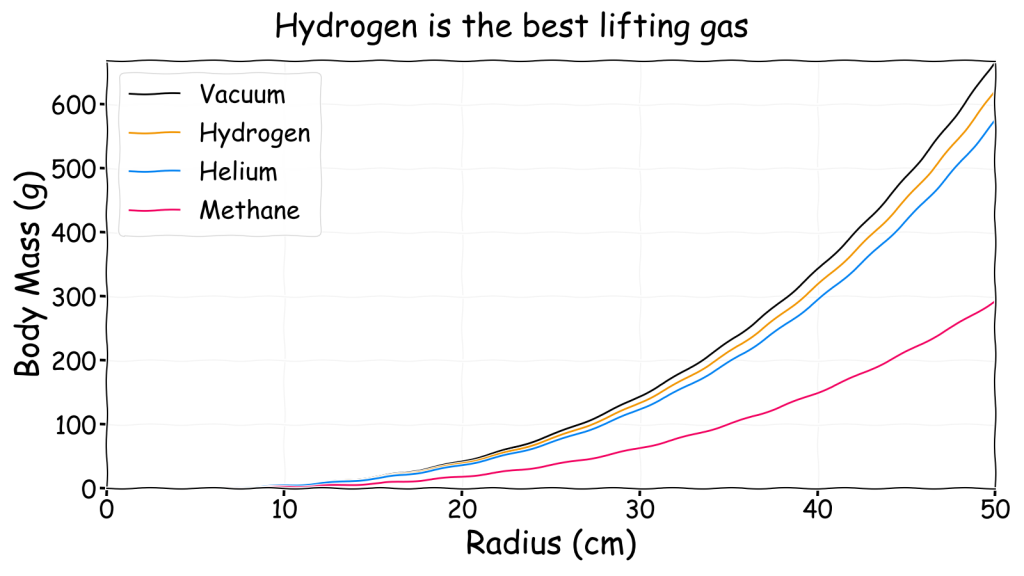
Note that the black vacuum curve represents the absolute best achievable without changing the ambient conditions. It has a zero mass lifting gas with a zero mass membrane, nothing can beat that. However, hydrogen is very close in lifting performance to vacuum so for all practical purposes hydrogen is the best choice. In contrast, methane is not as good. Even a massless membrane methane filled balloon 1 m across can only lift 300 g before it sinks to the ground. That’s something like a large grapefruit, a small rat or a human heart.

From this point on it will be assumed that the lifting gas is always hydrogen as it gives good lift and it can be produced biologically.

Membrane

The second parameter that can be changed is the membrane. Obviously a zero mass gas impermeable membrane would be ideal but that seems unlikely to be possible. Therefore, something lightweight is needed to keep the lifting gas and the ambient air from mixing. The exact nature of this membrane would vary significantly with gasbag size. A small gasbag would have a thin simple membrane but for a large gasbag the membrane would necessarily be thicker and more complex.

Referring back to equation 2 for the minimum radius required for neutral buoyancy, it is perhaps useful to know that using the STP densities for hydrogen and air the minimum required radius for neutral buoyancy is approximately 2.5 times the membrane area density (kg/m²). I.e. a membrane with a density of 1 kg/m² requires a balloon with at least a 2.5 m radius. This illustrate how a low membrane density is vitally important to reduce the size of gasbags.

For the smallest gasbags it is possible that the membrane is only a single cell thick. For a eukaryotic cell this will be assumed to be 10 μm thick and consist of water to give a density of 10 g/m². It is unclear how strong such a single cell membrane could be but it does provide a low density example for small gasbags.

The second example membrane is a metallised Mylar material as used in helium balloons. This apparently has an area density of around 25 g/m². It is not expected that a living organism would produce something identical to this but instead some form of lightweight impermeable membrane with similar qualities made from organic material.

Finally, the third example is based on the thin skin of a frog’s vocal sac. From a diagram in a scientific paper it seems that this skin is about 0.05 mm thick and if it is assumed to be made of water this gives a density of 50 g/m². For comparison this is about a tenth of the thickness of your eyelids which are the thinnest skin on your body.

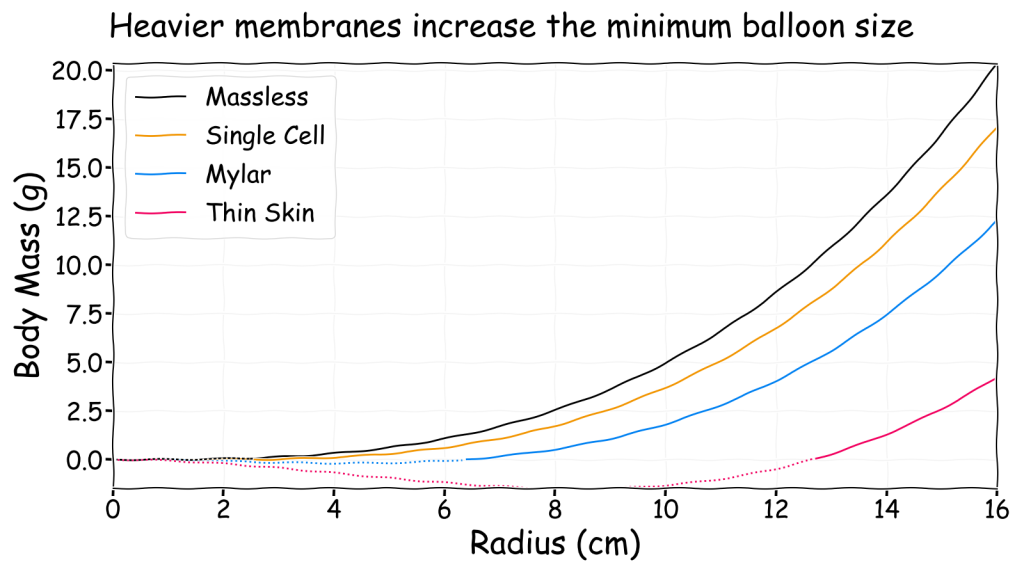
In the above chart a dotted line indicates that a balloon of that size is only neutrally buoyant with a negative mass payload. Since this is physically impossible a gasbag of that size with that membrane will never be lighter than air. For these three membrane materials with a hydrogen filled balloon on Earth here are the minimum radius values below which a gasbag can never float:

• Single cell: 2.5 cm
• Mylar: 6.3 cm
• Thin skin: 12.7 cm

Some people may be surprised at how large these values are. This is just a consequence of the lift from the graph being proportional to radius cubed (i.e. volume) whereas the weight of the membrane is proportional to radius squared (i.e. surface area). For this reason if you half the dimensions of a gasbag the lift drops by a factor of eight (i.e. 2 x 2 x 2) but the membrane weight only drops by a factor of four.

Despite what you may have seen in art and other media, small gasbags are generally not very viable. Even a very thin membrane can still only support a body weight of a few grams and it would be extremely fragile. Unsurprisingly, that is just like a helium balloon.

These neutrally buoyant minimum sizes would only support a very simple organism as there is no mouth, stomach or other organs present in the membrane. The common sky plant concept is perhaps the only viable option here as then there is no need for a body. A 2.7 cm radius eukaryotic algae bubble is perhaps almost plausible and a membrane of prokaryotic cells 1 μm in width would produce an even smaller minimum radius of 2.7 mm. A different approach is required to enable small but complex lighter-than-air gasbags on Earth but perhaps they are possible on other planets with different atmospheres?

From this point on it will be assumed that the lifting gas is always hydrogen contained within a membrane equivalent to Mylar.

Atmosphere

Perhaps the best way to make smaller gasbags more viable is to move to another planet where the atmosphere is denser and more suitable. If this is a real planet that you can simply look up the atmospheric density and repeat the calculations above. However, if it is not then you need an approximate way of estimating the density. This can be achieved using Boyle’s Law and Charle’s Law.

Boyle’s Law states that density is proportional to pressure. If air pressure is doubled then the density is also doubled. In contrast, Charles’s Law states that density is inversely proportional to temperature. If temperature (in Kelvin) is doubled then density will half.

To model this new atmosphere the following four step process is used:

1. Define atmosphere (composition, temperature and pressure)
2. Calculate atmospheric density at STP
3. Convert atmospheric density at STP to density at the real temperature and pressure
4. Converting lifting gas density at STP to density at the real temperature and pressure

The first step of defining an atmosphere can be quite complicated to do in a completely realistic way. This is an entire topic in itself, so will be left for another day. Slightly modifying a known planetary atmosphere is probably the simplest way of doing this.

The second step involves calculating the atmospheric density of the specified constituents if they were at STP. If this is an Earth-like atmosphere then just use the STP value of air. Otherwise calculate the atmospheric STP density calculating a weighted average of the individual densities according to their proportion of the atmosphere. For example with three gases (A, B, C)

\[\operatorname{density} = \operatorname{density\_A} * \operatorname{fraction\_A} + \operatorname{density\_B} * \operatorname{fraction\_B} + \operatorname{density\_C} * \operatorname{fraction\_C}\]

Wikipedia has STP density values for many gases but the following gases are sufficient for most atmospheres and it really isn’t necessary to worry about trace gases for this purpose.

• Earth air: 1.2754 kg/m³
• Carbon dioxide (CO₂): 1.977 kg/m³
• Carbon monoxide (CO): 1.250 kg/m³
• Helium (He): 0.179 kg/m³
• Hydrogen (H₂): 0.090 kg/m³
• Methane (CH₄): 0.716 kg/m³
• Nitrogen (N₂): 1.250 kg/m³
• Oxygen (O₂): 1.429 kg/m³

The third step involves rescaling the atmospheric STP density using the following relationship that combines Boyle’s and Charles’s Laws.

\[\operatorname{new\_density} = \operatorname{density\_at\_STP} * \operatorname{pressure} * \frac{273.15}{\operatorname{temperature}}\]

The temperature value must be in Kelvin and the pressure in bars.

The final step is to convert the density of the lifting gas (i.e. hydrogen) from STP to the same temperature and pressure as the atmosphere. This is because the pressure inside the balloon with be the same as that outside the balloon otherwise the balloon would expand or contract. Similarly, heat would flow through the thin membrane until the temperature was the same inside and out.

Using this process three alien atmospheres have been defined for comparison with Earth. Firstly, is the upper troposphere of Jupiter, which is just above the water clouds and expected to be the best location for photosynthesis. Secondly, is the temperate zone in the middle cloud layer of Venus 51 km above the surface. Finally, is the surface of Titan.

Location	Temperature Earth(K)	Pressure (bar)	Composition	STP Density (kg/m3)	Atmospheric Density (kg/m3)	Hydrogen Density (kg/m3)
Earth	273	1	Nitrogen: 78% Oxygen: 21% Argon: 1%	1.275	1.275	0.090
Jupiter	300	5	Hydrogen: 90% Helium: 10%	0.099	0.449	0.409
Venus	342	0.93	Carbon dioxide: 98% Nitrogen: 2%	1.962	1.457	0.067
Titan	92	1.4	Nitrogen: 94% Methane: 6%	1.218	5.060	0.373

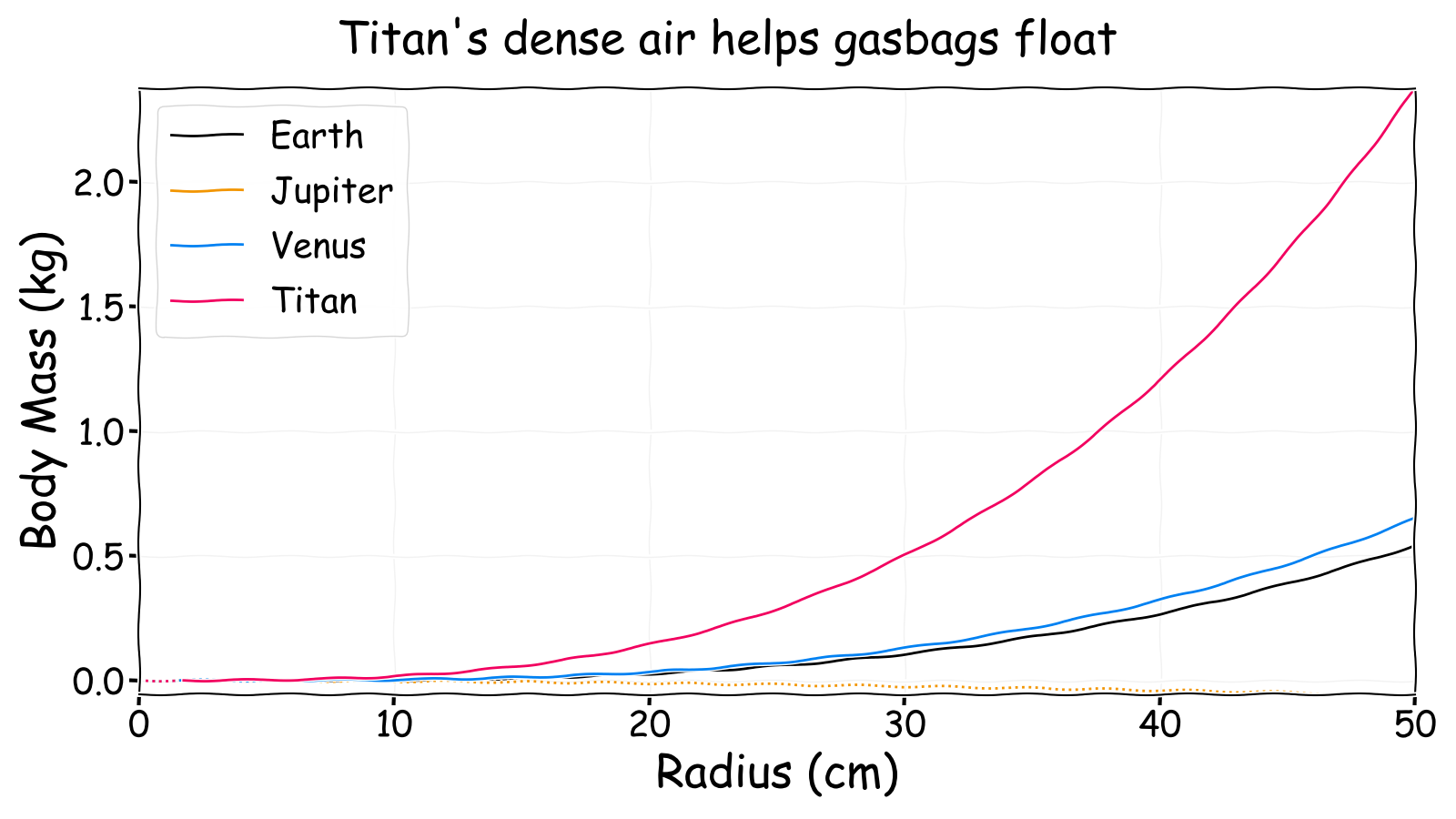
The first thing to note is that, perhaps surprisingly, Jupiter appears to be a suboptimal environment for gasbags. In fact, a hydrogen filled Mylar membrane must have a radius of 1.88 m before it is neutrally buoyant. This is because the lifting gas is hydrogen and the ambient air is mostly hydrogen so there is minimal density difference to produce buoyancy. That is why gasbags on Jupiter are usually described as being colossal (i.e. kilometres across) as even the smallest possible ones at this altitude are similar in size to an elephant.

Venus is slightly better than Earth due to an atmosphere mostly composed of the heavy gas carbon dioxide. A standard Earth air mix in the clouds of Venus would be a lifting gas despite the relatively close temperature and pressure conditions to Earth. This is why it has been proposed that floating cities filled with standard Earth air could be used to colonise Venus!

Finally, Titan is clearly a good place for gasbags despite having an atmosphere that at STP is slightly lighter than Earth air. This is because the high pressure and very low temperature combine to increase the density difference between the air and the lifting gas. This allows a greater body mass for the same size balloon. Even a 1.6 cm radius Mylar balloon (or a 6.4 mm radius algal sphere) could float on Titan.

From this point on it will be assumed that the lifting gas is always hydrogen contained within a membrane equivalent to Mylar floating in an Earth standard atmosphere.

Advanced Aspects

Balloons

As suggested by Charles’s Law and demonstrated by hot air balloons, it is also possible to gain lift by heating the lifting gas to reduce its density. This can be achieved by heating ambient air but perhaps heating hydrogen lifting gas would produce an extra benefit?

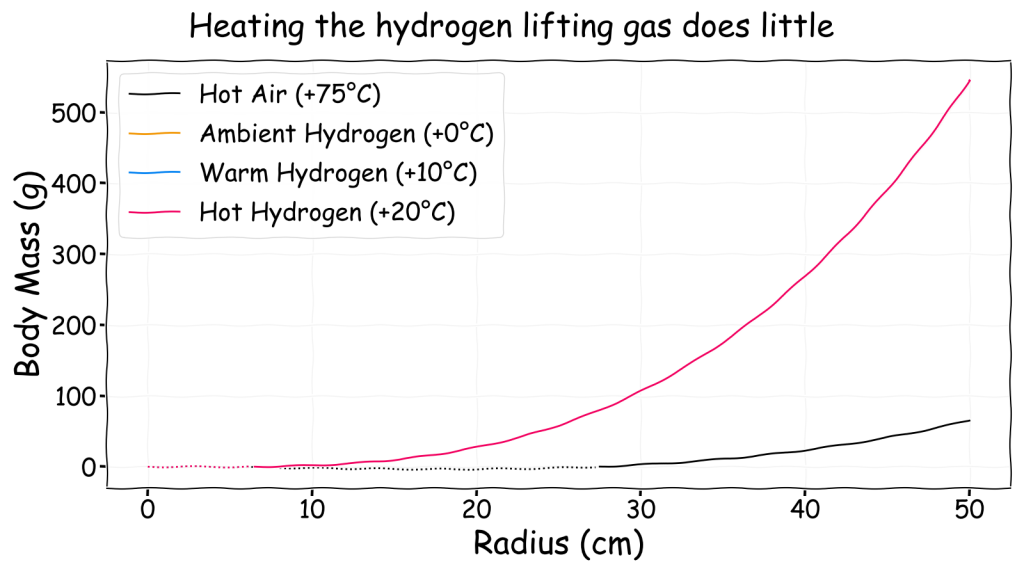
As can be seen, heating the hydrogen lifting gas by 10 or 20°C above ambient does so little that the curves on the chart are effectively identical. Furthermore, hydrogen provides much more lift at ambient temperatures than heating the ambient air by 75°C does.

Without even considering the problems of energy consumption and thermal insulation this suggests that heating the lifting gas is not a viable approach for a gasbag and simply using hydrogen is a far better approach in most cases. Perhaps an truly massive gasbag could gain some extra lift from warming its lifting gas simply through standard metabolic processes, though even then the effect wouldn’t be large.

Soap Bubbles

The previous analysis shows that large gasbags are always possible, however, due to the membrane, small gasbags may not be possible. To push this limit as far as possible the membrane mass has to be reduced significantly. One idea I had for doing this was for the gasbag to be based on a soap bubble and this idea was discussed in depth in my guest post on the Planet Furaha blog. There are plenty of videos on the internet of  hydrogen filled soap bubbles exploding, so clearly a bubble gasbag is potentially possible.

The basic idea is that since a bubble is made of water and only about 1 µm thick the membrane density is a very low 1 g/m². Unlike a solid membrane this would only be temporary, as eventually the water will evaporate and the bubble will pop when it is too thin. Under low temperature and high humidity conditions a bubble may last sufficiently long to be a viable temporary option though.

About a hundred years ago, in a sealed container it is claimed that Scottish scientist James Dewar managed to get a 19 cm diameter bubble to last for over three years and a 32 cm diameter bubble to last for 108 days. This is not likely under realistic conditions but it shows what is possible. Adding chemicals to the mix can make the membrane last longer. For fun at home the Soap Bubble Wiki has several recipes for this.

Obviously a single bubble would be very fragile and only suitable for the lightest body masses. An alternative approach would be to have a foam of many small bubbles each of which can generate some lift on their own. This approach has been used to generate floating helium filled foam letters for advertising purposes!

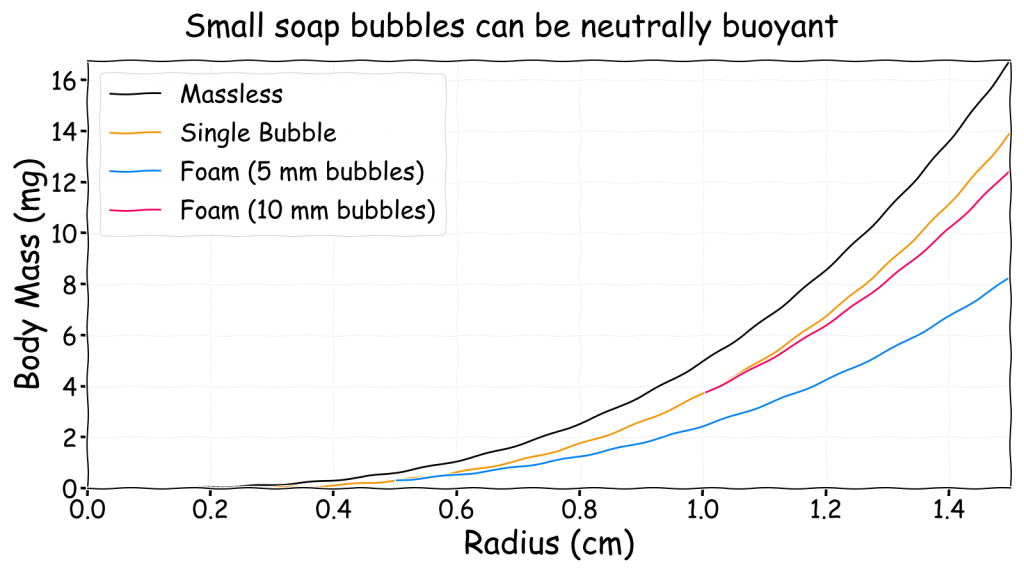
The chart above shows neutrally buoyant bubbles with a radius smaller than 1 cm are viable though can only lift a few milligrams. For context, ants weight between 1 and 5 mg so a balloon riding bubble-ant seems at just about plausible. Under Earth-like conditions the smallest viable bubble has a radius of about a quarter of a centimetre. Bubbles smaller than this are still possible and they may even float on updrafts but it is not possible to make them neutrally buoyant by filling them with hydrogen even though they will be lighter.

Graphene

The final option (also discussed in a guest post on Planet Furaha) for improving the viability of small gasbags relies on the wonder material graphene that was discovered in 2004 by scientists at the University of Manchester who subsequently received a Nobel prize for their work.

Graphene is an allotrope (i.e. a different structure) of carbon made of a flat sheet of atoms connected in a hexagonal pattern. It has many interesting properties including high strength (100 times stronger than steel) and low density (less than 0.001 g/m²). An amusing illustration of this was provided in the Nobel prize paper. A 1 m² graphene hammock tied between two trees could hold a 4 kg cat before breaking yet would only weigh as much as one of the cat’s whiskers.

The important property for gasbags though is that recent work suggests graphene is also impermeable to gases. With such an amazingly low density it effectively produces a matte-black massless membrane even when many layers are used.

It would likely be impossible for life to produce large balloons made of a few layers of defect free-graphene but perhaps the bubble foam concept can be used to produce a mass of small hydrogen filled graphene bubbles? Conveniently, a material extremely similar to this called aerographene has already been invented by scientists. It consists of a complex 3D network of graphene and carbon nanotubes where most of the volume is air. For this reason, when measured in a vacuum it has a density slightly lower than helium at 0.16 kg/m³.

Aerographene itself is not airtight but it is not inconceivable that a material like it could be produced that contains many small airtight compartments in a similar way to a bubble foam. If these compartments contained a lifting gas, then the entire structure would float. From this point on when I mention aerographene I am actually referring to this possibility and not the real material.

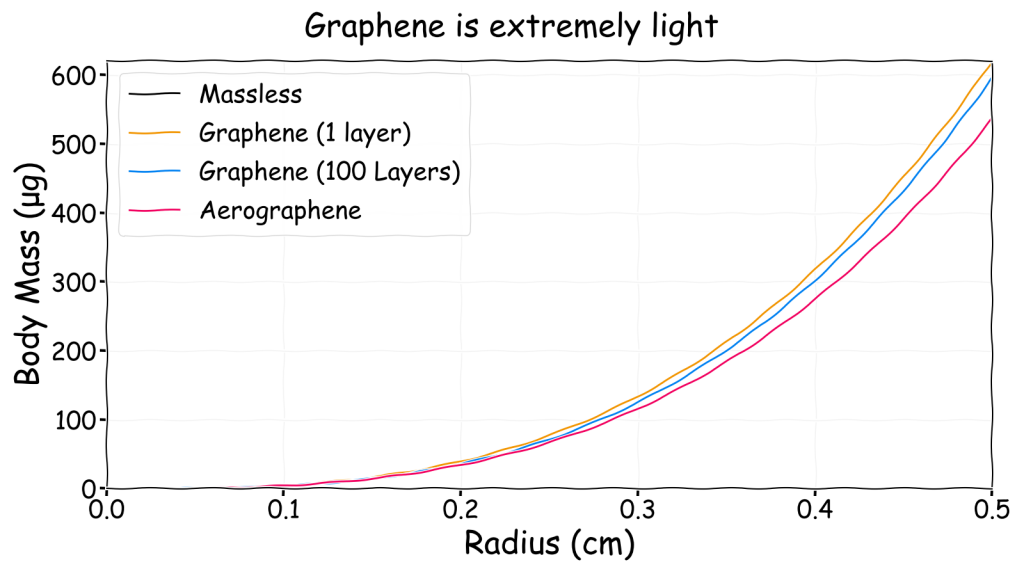
The obvious point to note from this chart is that the black massless curve is completely obscured by the single layer graphene curve. This illustrates how light graphene is. This chart also shows that extremely small (sub-mm) neutrally buoyant gasbags are possible using graphene unlike with any other identified membrane material. It is perhaps skirting the edge of what is known to be possible but it is somewhat based on actual science within the rapidly changing world of graphene.

Body Size

Up to this point I have considered the mass of the gasbag’s body in relation to the balloon’s size. However, this doesn’t always give the best idea of what a gasbag might look like and that is very important for artists. So the question then becomes, how large is the gasbag’s body?

As I mentioned before, since I am physicist I will assume the gasbag’s body is a sphere of “mostly water” hanging underneath a balloon of “mostly gas”. This means it has a density of around 1000 kg/m³. Obviously a real body isn’t spherical and will likely have tentacles, fins, etc. It’s a good enough approximation to get an idea of size though.

\[M_b = \frac{4 \pi R_b^3}{3}\rho_b\]

\(M_b\) is the body mass, \(R_b\) is the spherical body radius and \(\rho_b\) is the body density, which is equal to the density of water (1000 kg/m³). Using this approximation the following charts shows how the membrane radius (in metres) is related to the body radius (in centimetres) for a hydrogen filled Mylar balloon in the four previous locations.

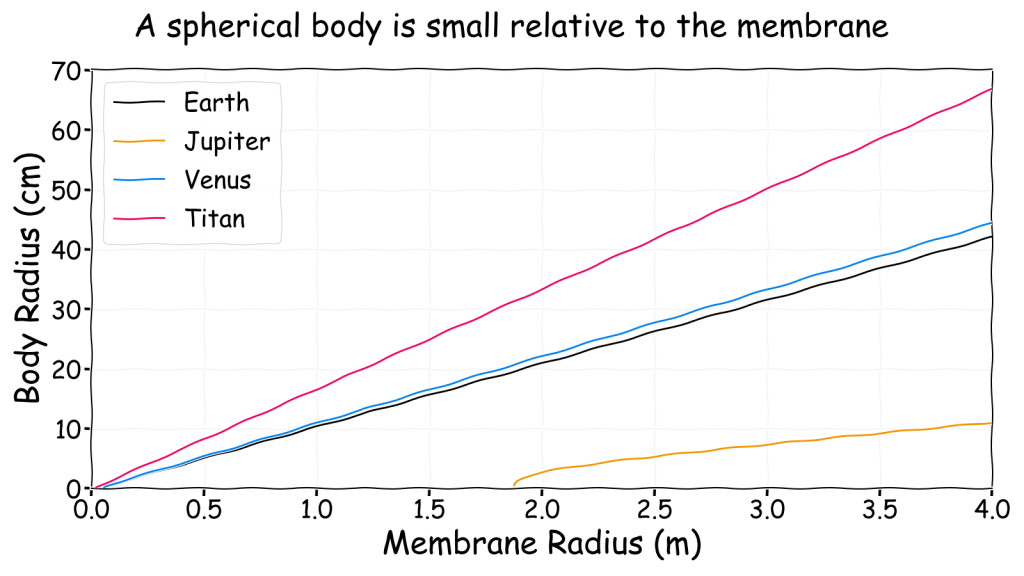
This shows that even a large balloon can only support a small body, though it would appear larger if it were not a sphere and was spread out instead. Ultimately, a gasbag is only viable if it actually looks much like a normal balloon. The sky whale notion where something that looks like a fish can actually float in the air does not appear to be very plausible. A better comparison can be found by calculating the radius of the body as a proportion of the radius of the membrane

This shows that for gasbags significantly above the minimum size the radius of the spherical body remains proportional to the membrane size regardless of size. This is handy feature as it enables a basic rule of thumb such as, on Earth a large hydrogen filled Mylar balloon can lift a body that is just over 10% of the width of the balloon. This 10% value is a function of the density difference between the air and the lifting gas. Therefore it can be calculated for any environment to produce an approximate guideline. Note that for sufficiently large gasbags it is also independent of membrane density.

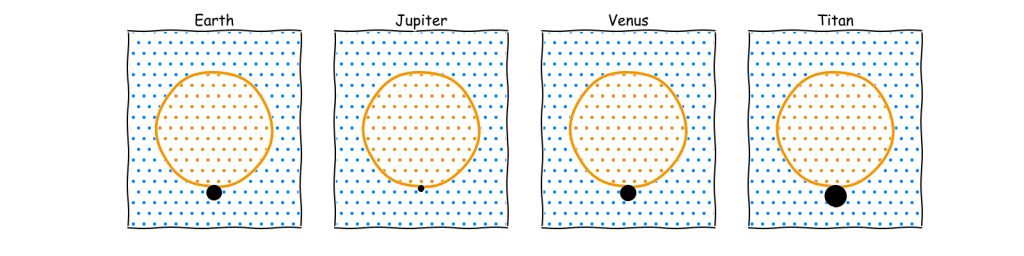
The image above is absolutely key to gasbags as it provides a reference to how large the body can be relative to the balloon which for sufficiently large balloons is independent of size and membrane. The only way to make the body larger is to change the atmospheric density as there is no better lifting gas than hydrogen. For anyone drawing a gasbag, be sure to make the body as thin and spread out as possible if you want to remain with plausible limits.

Summary

Lighter than air organisms are a common trope in speculative evolution despite never having evolved on Earth. However, the amount of lift generated by a balloon of a certain size is often significantly overestimated. This first post on gasbags focused on the physics of buoyancy which is relatively simple and can be used to estimate a gasbag’s size versus mass under various conditions.

A simple model of a floating gasbag uses the following four parameters to calculate the neutrally buoyant body mass that the gasbag’s balloon can lift:

• Balloon size
• Lifting gas density
• Ambient air density
• Membrane area density

While the full analysis of these parameters was quite lengthy, it produced several key conclusions that can help create plausible gasbags for speculative evolution and world building:

• Gravity does not directly influence the lift produced.
• Lift is generated by the difference between the ambient air density and the lifting gas density.
• The weight of the balloon membrane reduces the net lift.
• Larger gasbags produce more lift.
• Hydrogen is the best lifting gas.
• Gasbags are more viable in high density atmospheres (i.e. Titan) and less so in low density atmospheres (e.g. Jupiter).
• The weight of the membrane causes a minimum size below which a gasbag cannot float.
• In Earth-like conditions the minimum balloon radius (m) is approximately 2.5 times the membrane density (kg/m²). 
• Heating the lifting gas to gain lift is unlikely to be viable.
• Bubbles and graphene may allow very small gasbags.

It is difficult to summarise all of these parameters in a useful way but hopefully I have already presented enough information to allow you to estimate the appropriate gasbag size for your own environment. However, the following log charts are probably the best way to present data over a wide range of values but they can be difficult to interpret if you are not familiar with them. Please add a comment to this post if this is not sufficient and I may be able to help.

In the first chart, the minimum balloon size versus membrane density can be presented for each of the four locations. Marked on the chart are four example membranes to provide some context. Graphene is not on the chart as its density is less than 0.001 g/m² which places it far off the left hand side. For even larger gasbags a thicker membrane is probably required. Perhaps this should be 1 cm thick (i.e. the size of the smallest vertebrates) and have a density of 10 kg/m². This would be far off the right hand side of the chart instead.

In the second more complicated chart, balloon size is linked to body mass for four different membranes in each of the four locations. The mass of a variety of airborne animals is included to provide an estimate of a plausible gasbag. Note that on Jupiter a Mylar balloon just under 2 m in radius is only just sufficient to lift a housefly! If it is smaller than this it would actually be heavier than air and sink until it reached a deeper, denser region. Even on Earth an 8 cm radius Mylar balloon is required which shows just how unlikely small gasbags really are. This problem was what drove the need to consider bubbles and graphene as possibilities.

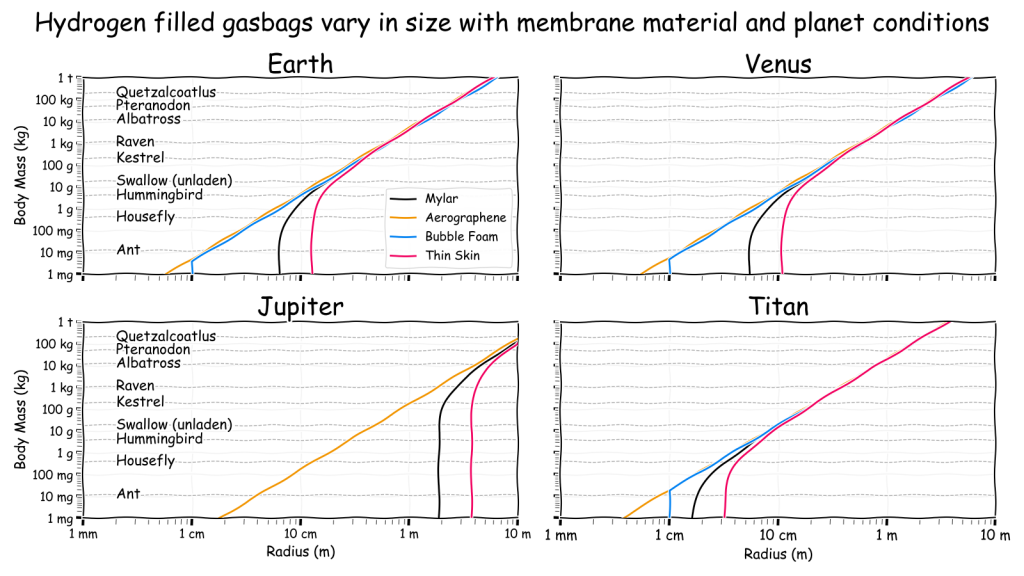
In all of this it is worth stating that I use the xkcd style charts to illustrate that this is about providing estimates of plausibility and not hard qualitative science. After all, we are not building a lighter-than-air survey probe to explore another planet but we do want any speculation to be grounded in known scientific principles. Hopefully what I’ve written can help people achieve that.

Despite the length of this post, the basic physics of buoyancy is only one consideration in designing a plausible gasbag. There are other considerations such as:

• Where does the lifting gas come from?
• How does it gather energy and nutrients?
• What method is used to control its altitude and motion?
• Most importantly, how could such a create evolve?

Questions such as these will be addressed in a following post on this subject. Please let me know in the comments if you have any questions relating to those subjects and perhaps I will have time to include them in the article.

Finally, thank you to Richard Bizley (bizleyart.com) for providing some of the images used in these posts about gasbags so they aren’t entirely dominated by my charts. Check out his web site for many pictures that might provide inspiration and you could even buy a print too.