After a long break, I am finally continuing the series on gasbag life. Firstly, I discussed the physics of lighter-than-air floating life that relies solely on buoyancy. Then, the possibility that small heavier-than-air aeroplankton could sink slowly enough that updrafts could keep them in the air. There is a third approach that gasbag life could take. By combining aerostatic and aerodynamic lift a more active hybrid gasbag body plan is enabled. Such a body plan partially offsets gravity using a lifting gas but relies on motion to produce the remaining lift.

Summary
The basic idea in the first three articles is to consider something similar to the three classes of organisms identified in Carl Sagan’s 1976 NASA report on Jupiter: floaters, sinkers and hunters.
In the following discussion we will consider three comparable ecological niches on Jupiter: The primary photosynthetic autotrophs, which must replicate before they are pyrolyzed, will be described as sinkers. A second category of larger organism which may be either autotrophs or heterotrophs but which actively maintain their pressure level will be described as floaters. A third category of organisms actively seek out other organisms; we call these hunters, although, as we shall see, the distinction between hunting and mating under these conditions is not sharp.
Carl Sagan, Particles, environments and possible ecologies in the Jovian atmosphere (1976)
Sinkers are the foundation of an aerial ecosystem and consistent of very small light aeroplankton that can float on the ambient updrafts. This allows them to remain in the air long enough to reproduce and therefore become smaller and lighter again.
Floaters are larger organisms that use lighter-than-air lifting gas to inflate a balloon to counteract gravity. Due to the weight of the membrane there is a minimum size where this approach is viable. Therefore floaters can range from small to truly gigantic sizes, though may still be planktonic (i.e. they travel with the wind and have minimum control over motion).
The hybrid gasbag category uses a lighter-than-air lifting gas to partially counteract gravity (i.e. aerostatics). However, the remaining lift is generated from the flow of air over its body in the same way as a plane operates (i.e. aerodynamics). This category is suited for more active medium sized organisms as it requires the ability to generate thrust.
Real Life Inspiration
Sharks
Marine animals provide one example of this hybrid approach in real life. Bony fish have a swim bladder that effectively acts as a gasbag to provide buoyancy. By adjusting the gas within the bladder the fish can remain neutrally buoyant at a range of depths. However not all fish have swim bladders.
For example, cartilaginous fishes (e.g. sharks) don’t have one. Sharks do however have large livers filled with an oil less dense than water. This provides some buoyancy (i.e. hydrostatic lift) but not enough to entirely counteract gravity. Sharks therefore have to rely on hydrodynamic lift to remain at a constant depth.
One method sharks can produce lift is by using their pectoral fins as “wings”. The tail provides thrust which produces forward motion and the resulting flow of water generates lift from the fins. This is analogous to fixed wing aircraft. Undoubtedly the shape of the shark’s body also provides lift to add to the hydrostatic buoyancy.

Hybrid Airships
This concept has also been applied above water via hybrid airships. In a similar fashion to sharks, the helium filled envelope does not generate sufficient lift to balance the weight of the airship. Therefore, in the absence of further lift it would fall slowly from the sky. In fact, it would not even be able to take off in the first place.
However, if the airship envelope is moving relative to the air it can be used to generate aerodynamic lift. This aerodynamic lift can combine with the aerostatic lift to completely oppose gravity. The amount of lift is proportional to the air speed squared so the airship must be moving relative to the air surrounding it.
The final requirement for a hybrid airship is therefore a source of thrust that can move the airship through the air. The forward motion will then produce the lift necessary to keep the airship in the sky. This is typically provided by vectored thrust using ducted fans. This allows the force to be directed to produce forward motion, vertical lift or some combination of the two. This capability allows the airship to hover in still air despite not being neutrally buoyant.
An example of a hybrid airship is the Airlander 10 from Hybrid Air Vehicles. Due to its shape it has been nicknamed the “flying bum”! It is quite large and can carry 10 tonnes of cargo. Perhaps it is useful inspiration for the infamous “sky whale”?
- Length: 92 m
- Width: 43.5 m
- Height: 26 m
- Volume: 38,000 m3
- Maximum Weight: 33,285 kg
- Cruising speed: 148 kph

Shape Evolution
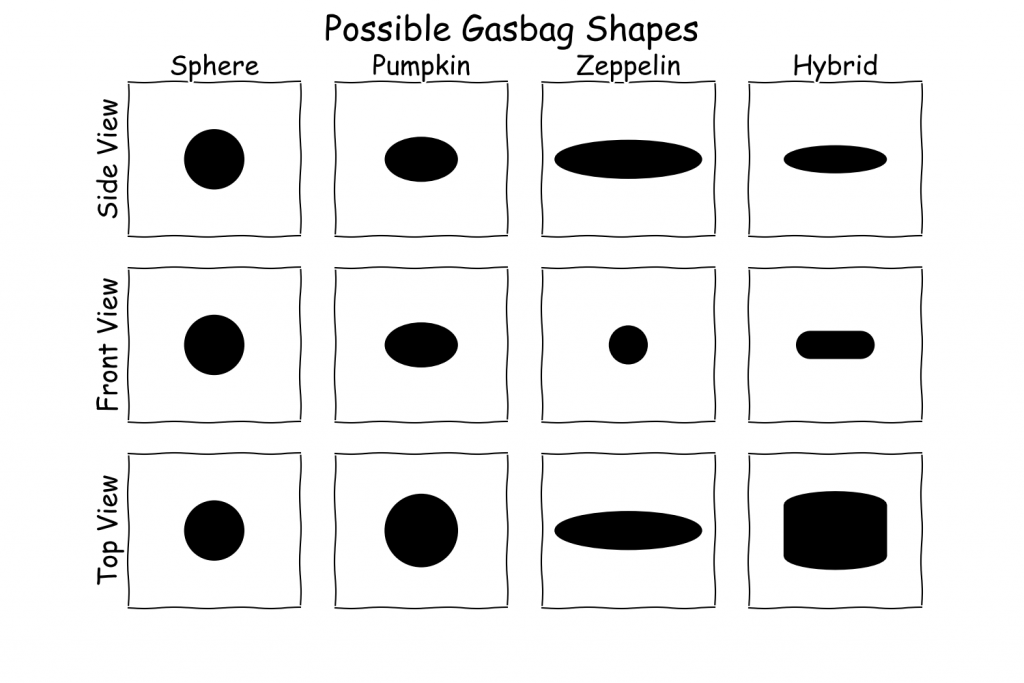
Before diving into technical details it is worth considering the evolutionary path that could lead to a hybrid gasbag. As discussed in the previous article about aeroplankton a small sphere can float on updrafts but if it gets a bit larger (> 3 mm diameter) a hydrogen filled sphere can potentially float in still air with a thin membrane.
A sphere is the ideal shape as it maximises the volume of lifting gas for a given weight of the membrane surrounding it. A sphere is therefore the optimal shape for a small simple planktonic lifeform.

In order to maintain this shape it is necessary to have a slightly higher pressure inside than outside. Such a balloon is called a superpressure balloon. As the sphere becomes larger the pressure needed to maintain the spherical shape becomes too great. This limits spherical superpressure balloons to smaller sizes.
A century ago an alternative design using meridional (i.e. top to bottom) tendons to carry the load was proposed. Between each pair of tendons is a gore of membrane that bulges out slightly under pressure. This allowed larger super pressure balloons to be produced that formed a natural pumpkin shape when stress was equally distributed.

Such a pumpkin shaped gasbag could grow larger than a spherical gasbag but it would not be efficient at moving. For faster motion a gasbag could reduce drag by becoming more streamlined so that less thrust would be required to move through the air.
The simple way to achieve this is to take on an ellipsoid shape with a circular cross section and a long axis in the direct of motion. This is approximately the shape that traditional airships take. In order to reduce the drag the UK National Physics Laboratory produced a standard low drag design which has a fineness ratio (length divided by diameter) of four. Perhaps a sphere could elongate into this form?

However, for the hybrid approach it is necessary to increase the width and decrease the height to improve the aerodynamic lift. This could be achieved by stretching a zeppelin sideways or by widening a pumpkin in one direction. The approach taken by hybrid airships is a multi-lobe design. Conceptually, multiple ellipsoids with circular cross sections are placed side-by-side with some overlap. For simplicity this can be treated as a single ellipsoid with an elliptical cross section though.
For comparative purposes these four shapes will be used as the archetypical gasbag shapes, though the exact hybrid gasbag shape is variable. There will of course be additional wings, fins, tails, tentacles, etc. which I won’t consider here.
Physics
I had originally intended to produce some useful equations on the combined aerostatics and aerodynamics of hybrid gasbags. Unfortunately, and not unexpectedly, it turns out to be quite complicated! While it has been quite interesting researching this area at some point it becomes too complex to be a useful rule of thumb for worldbuilding and speculative evolution. Therefore, I’ll just give an overview of the basic principles involved and provide some charts that will hopefully provide useful guidelines to others.
Copying the approach taken by hybrid airships there are five forces to consider:
- Aerostatic lift: Generated by lifting gas and always present
- Aerodynamic lift: Generated by body shape when moving relative to the air
- Gravity: The omnipresent force pulling the gasbag down
- Vectored thrust: Generated by body motion in a semi-arbitrary direction, though mostly relevant for forward motion but can be used for lift
- Drag: The resistance of the atmosphere to motion any direction, though typically represented as opposing thrust
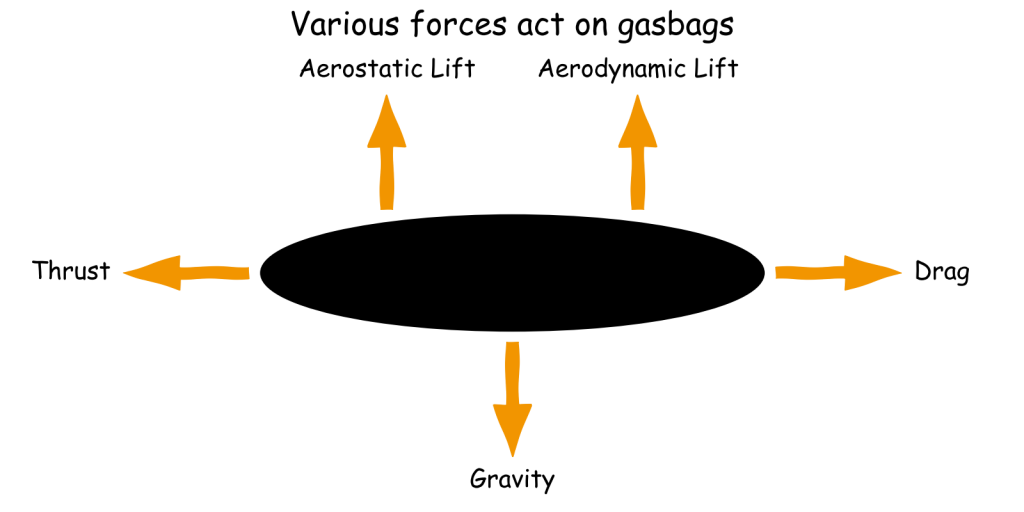
In order to remain at a constant altitude the following relationship must be true:
\[F_g = F_{as} + F_{ad} + F_{vt}\]
where \(F_g\) is the downward force due to gravity, \(F_{as}\) is the upward aerostatic lift, \(F_{ad}\) is the upward aerodynamic lift and \(F_{vt}\) is the vertical component of the vectored thrust. For pure gasbags \(F_{ad}\) and \(F_{vt}\) are equal to zero. Similarly for birds \(F_{as}\) is effectively zero whereas \(F_{ad}\) and \(F_{vt}\) vary depending on whether the bird is flapping or gliding.
For hybrid gasbags all three components are potentially relevant, however, for simplicity it will be assumed that vectored thrust (i.e. flapping wings) will not be used for lift in general. This is analogous to large birds that typically glide. Instead some fraction of the downward gravitational force will be balanced by aerostatic lift and the remainder will be balanced by aerodynamic lift.
This leads to the following two relationships when the gasbag is neither ascending nor descending:
\[\begin{align}F_{as} &= \beta F_g\\F_{ad} &= (1-\beta)F_g\end{align}\]
where \(\beta\) is the buoyancy ratio that defines the proportion of total lift generated by aerostatic lift. This is typically at least 60% but more often 80%.
Aerostatics
The physics of aerostatic lift was covered in the first article on gasbags. The general concept is that to achieve aerostatic lift the overall density of the organism should equal the density of the surrounding air to be neutrally buoyant. This is achieved by adding a large balloon filled with a lighter-than-air lifting gas to the body mass. The greater the density difference between the inside and outside of the balloon the more body mass can be carried for a given balloon volume.
For simplicity I will include the weight of the lifting gas in the equation for the buoyancy force (i.e. it reduces the buoyancy force) but formally this should actually be part of the gravitational downward force. It is however easier to only consider the mass of the organism’s body for the gravitational force as that allows an easier comparison with Earth animals.
This leads to the following relationship for the upward buoyancy force:
\[F_{as} = gV\Delta_\rho\]
where \(g\) is the gravitational acceleration, \(V\) is the volume of the lifting gas only and \(\Delta_\rho\) is the density difference between the air and the lifting gas.
Aerodynamics
In contrast, the area of aerodynamics is vastly more complicated. Simplistically, the shape of the gasbag can be used to calculate the lift and drag produced as it moves through the air. This is represented by the lift coefficient (\(C_L\)) and the drag coefficient (\(C_D\)). To further complicate things, the lift coefficient is a function of the angle of attack of the gasbag. This means pointing the nose up will increase lift.
However, the drag coefficient is also a function of the lift coefficient, so generating lift unavoidably generates drag. The relationship between the two coefficients as a function of angle of attack is shown below. The optimum point can be found where the lift-to-drag ratio is maximised. At this angle, the minimum amount of thrust (and therefore energy) is required to generate the required amount of lift.
\[\begin{align}C_L &= \frac{C_{L\alpha}\alpha S}{V^{2/3}} \\ C_D &= C_{D0} + K{C_L}^2\end{align}\]
where \(C_{L\alpha}\) is the lift slope, \(\alpha\) is the angle of attack, \(S\) is the cross-sectional area of the gasbag that produces lift, \(V\) is the gasbag volume, \(C_{D0}\) is the zero lift drag coefficient and \(K\) is the lift induced drag factor.
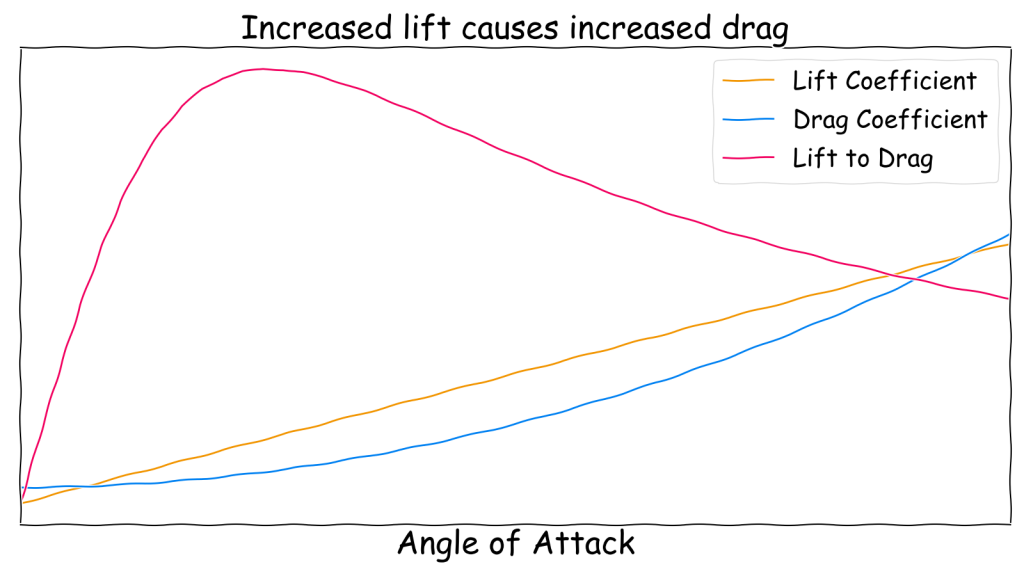
At this point it should become clear how complicated the situation is. I won’t go into further detail here, but for a better understanding you can read A comparative study of conventional and tri-lobed stratospheric airships. Note that this assumes an ellipsoidal airship. Since this is symmetric it can only produce lift for angles of attack above zero. In practice this should be an aerofoil shape which can produce lift even at zero angle of attack.
The final step in this process is to calculate the actual lift force. This is required since we want the actual aerodynamic lift to be sufficient to balance gravity when combined with aerostatic lift.
\[F_{ad} = \frac{1}{2}\rho u^2 {V^{2/3}} C_L\]
where \(\rho\) is the air density, \(u\) is the air speed and \(V\) is the volume.
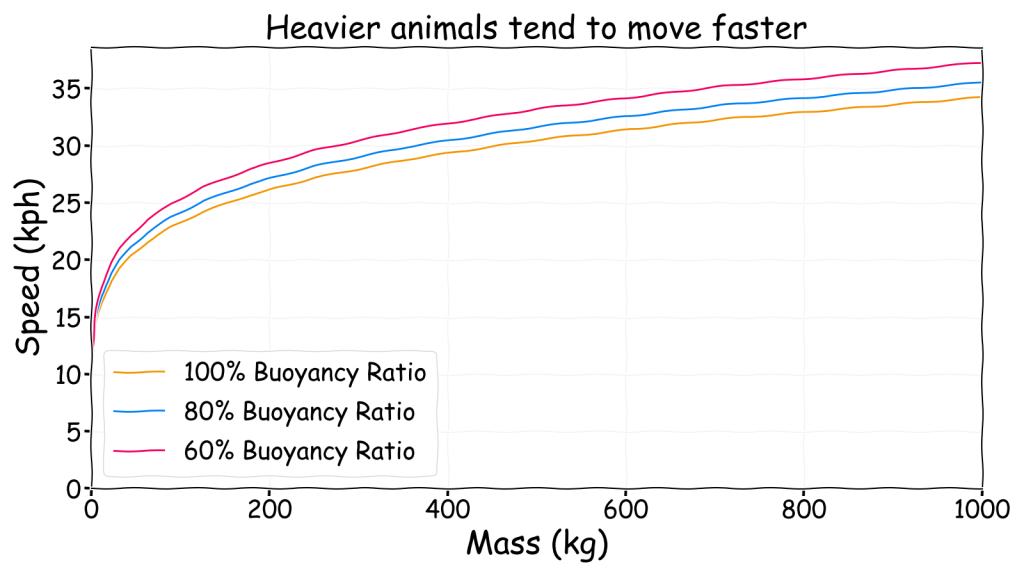
Calculating the air speed is another tricky step. Trying to define the muscle power required to achieve a certain speed seems far too complicated. Conveniently, there are some simple scaling laws that can be used to estimate speed. Unifying constructal theory for scale effects in running, swimming and flying provides approximate relationship that links body mass with speed.
\[\begin{align}u &= \left(\frac{\rho_b}{\rho_a}\right)^{1/3} g^{1/2} {\rho_b}^{-1/6} M^{1/6} \\
&= \beta^{-1/6} g^{1/2} {\rho_a}^{-1/6} M^{1/6} \end{align}\]
where \(u\) is the speed, \(\rho_b\) is the body density of the animal, \(\rho_a\) is the air density, \(g\) is the acceleration due to gravity and \(M\) is the animal’s mass. The resulting speed might seem a bit fast but the approximation apparently works quite well for flying and swimming animals on Earth. This can be modified for gasbags to replace the body density with the buoyancy ratio, \(\beta\).
\[u = \beta^{-1/6} g^{1/2} {\rho_a}^{-1/6} M^{1/6} \]
Thrust
Little needs to be said about thrust as the gasbag is assumed to generate sufficient thrust to overcome drag and reach the estimated speed. The most likely way to achieve this is with a tail and/or body motion like marine animals, perhaps with a variety of forms of locomotion like fish. This has even been demonstrated for an 8 m airship by using dielectric elastomer actuators.
Wing-like fins are also an option, though unlike birds these would primarily be for generating thrust and not for lift, since that comes from the aerofoil body shape. Maybe wings like a dragonfly are more likely to allow thrust to be supplied in any direction like the fans on an airship?
Perhaps jet propulsion using a siphon like a squid is even possible if the atmosphere is thick enough, though that is an investigation for another day.
Model
It is difficult to produce convenient rules of thumb for a multi-lobed hybrid gasbag shape made from multiple ellipsoids. This is complicated by the range of possible parameters that can all influence the final shape. The most useful approach seems to be to generate multiple sets of random parameters and calculate an optimal shape that maximises the lift-to-drag ratio for a fixed 80% buoyancy rate hydrogen filled gasbag in an Earth-like atmosphere.
These factors include:
- Mass
- Length to height ratio (fineness) for the individual ellipsoidal lobes
- Number of lobes (with fractional lobes possible)
- “Rigging” factor to represents tentacles, fins and other body parts increasing drag
- Slowness factor to represent slower moving gasbags
The dimensions of the resulting set of random gasbags can then be compared to those for a neutrally buoyant sphere, pumpkin and zeppelin. Note that the “zeppelin” is really the UK National Physical Laboratory’s low drag ellipsoid with a fineness (\(\lambda\)) of 4.
| Parameter | Sphere | Pumpkin | Zeppelin |
|---|---|---|---|
| Length (\(L\)) | \(2\left(\frac{3V}{4\pi} \right)^{1/3}\) | \(2\left(\frac{V}{2.7458} \right)^{1/3}\) | \(\left(\frac{6\lambda^2V}{\pi} \right)^{1/3}\) |
| Width (\(W\)) | \(L\) | \(L\) | \(L/\lambda\) |
| Height (\(H\)) | \(L\) | \(0.5991L\) | \(L/\lambda\) |
| Volume (\(V\)) | \(\frac{\pi}{6}L^3\) | \(\frac{2.7458}{8}L^3\) | \(\frac{\pi}{6\lambda^2}L^3\) |
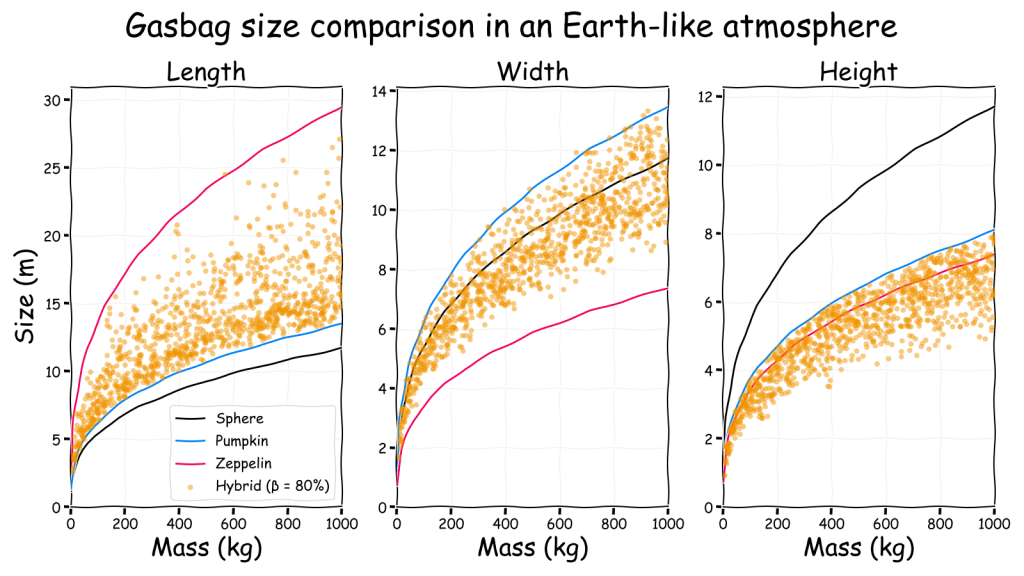
The simple interpretation of this is that hybrid gasbags can be a wide range of sizes. However, for the same body mass they will be somewhere between a zeppelin and a pumpkin in both length and width. In contrast, their height will be less than a pumpkin and probably less than a zeppelin too. In retrospect, perhaps that is obvious…
As expected, hybrid gasbags tend to be long and wide but not very tall, so they are basically flying pancakes or squashed pumpkins!
Possibilities
Maybe the outcome of all of this wasn’t entirely unexpected. Hopefully it does still give people some inspiration for producing lighter-than-air speculative life that isn’t just a sphere or a zeppelin shape though. The hybrid approach combining aerostatic and aerodynamic lift does seem to be a natural evolution of a gasbag as it becomes larger. If it is going to take on a more active lifestyle and move around then it might as well use its body to produce lift.
An interesting, and perhaps inevitable, possibility is that a gasbag could exert itself to accelerate and gain lift so that it can reach higher altitudes where the air is thinner. Perhaps it aims to rise out of the thick clouds and access sunlight. Or perhaps it hunts the high altitude photosynthetic gasbags. Then, when it is done, it can stop exerting itself and rely solely on aerostatic lift. It will then sink to lower altitudes where the air is thicker and it reaches neutral buoyancy again. Here it can rest and conserve energy before the cycle begins again. This strategy has actually been proposed for the Venus Atmospheric Maneuverable Platform (VAMP) mission concept.
There are many other possibilities which could be explored further too:
- The ground effect can be used to reduce drag when flying at very low altitude. Perhaps a sea skimming hybrid gasbag as considered in 1977 for a transatlantic cargo airship.
- The number of lobes could increase while the gasbag becomes wider and shorter until it resembles an inflatable flying wing.
- Fixed wings could grow larger to become a blended wing body like a manta ray.
- These wings could grow even larger to produced a winged airship, though this may not provide an advantage.
I’ll leave these possibilities for someone else to develop but there are definitely more possibilities than just flying pumpkins for gasbag life!
Acknowledgments
Thank you to Dr. Baraniello of Centro Italiano Ricerche Aerospaziali (CIRA) for providing access to some of his research for background reading. Also, thank you to Richard Bizley (bizleyart.com) for providing some of the images used in these posts about gasbags. Check out his web site for other pictures that might provide inspiration and perhaps even buy a print too.

Hello abbydon id like to discuss how plausible my ideas for a gasbag are for my spec evo project
If you have time ofc